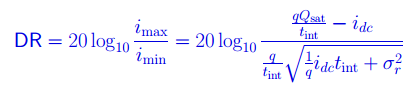May 21, 2016 · 1 minute read · Comments
hardwaresoftwaresystem
本文系微信公众号『大话成像』,知乎专栏『All in Camera』原创文章,转载请注明出处。
上一篇说到bm3d等高级算法可以利用数学方式把信号分解成不同性质的部分,然后根据不同的噪声特点进行去噪。噪声模型则是去噪算法的重要依据。
先看一个实验,拍摄一张Grey Scale Chart:

曝光时间 33ms, ISO 3200,得到如下图像:

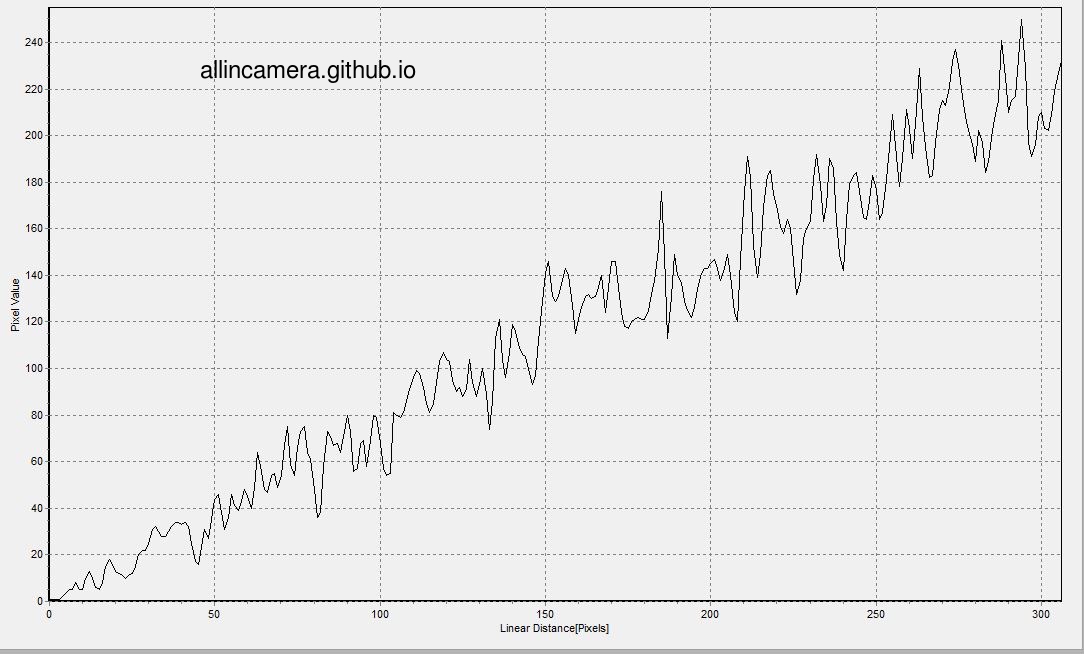
图像上有很多噪声,对这个图像做横切,可以得到pixelvalue相对intensity的关系图

继续拍摄至N张照片,将N张照片求平均得到一张照片
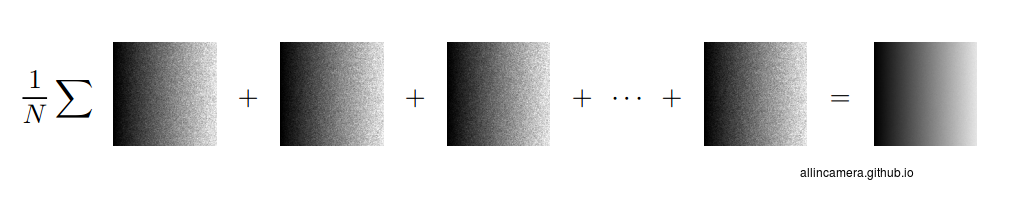
求和平均得到的照片

把所有图片的像素值与亮度标在一个图中
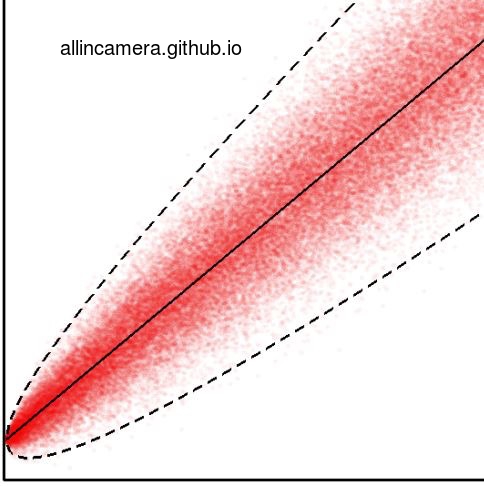
中间的实线是图像均值,所有被虚线包围的红色的点,是所有图像的像素值。
按照图解噪声与去噪第一篇里的方法,画出像素标准差对均值的曲线可以得到
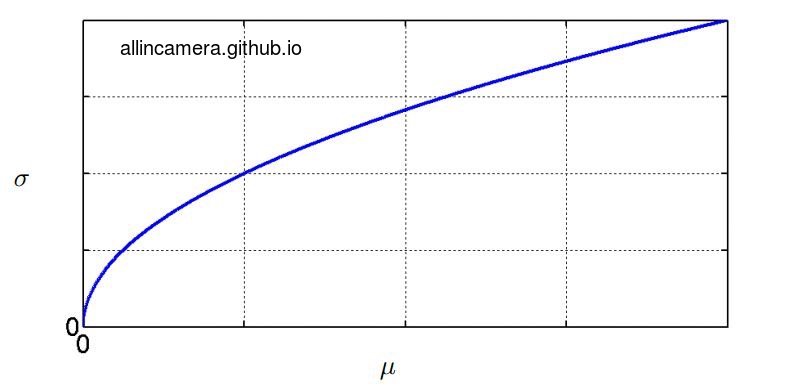
从上图可以看出:
1. 噪声随着亮度的增加而增加。
2. 标准差与均值遵循一定的函数关系。
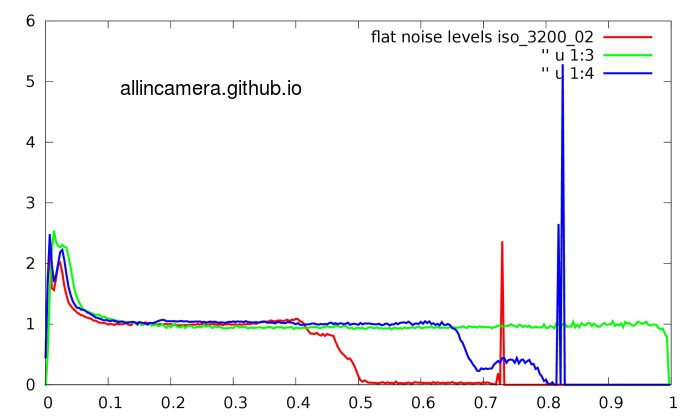
把多组实验的结果叠加可以得到下图:
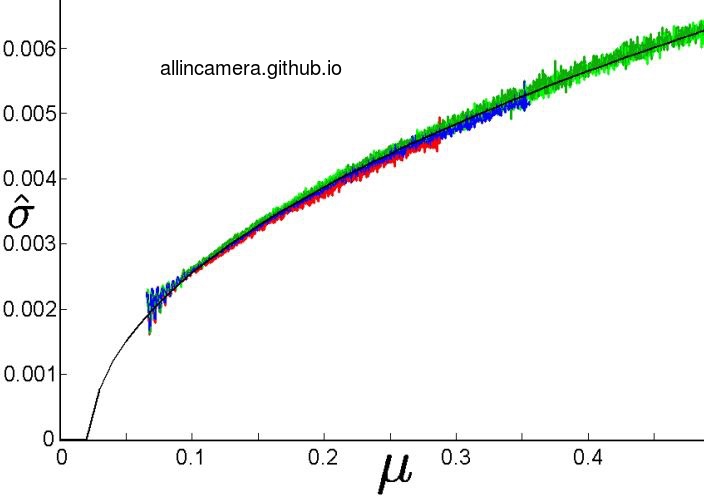
可以看出在平滑的曲线上多了许多毛刺.
从上面两张图可以看出在图像中存在着两种噪声:信号相关噪声,信号不相关噪声。平滑上升的曲线是随信号均值上升的,而毛刺是不随信号均值增大的。
数学上把这两种噪声用泊松分布模型和高斯分布模型来描述:
y = α Pi + ni, pi ~ P(x), Ni ~ N(0,σ2),
y是总噪声,α是量化参数,Pi是泊松噪声,Ni是高斯噪声,x是信号。Pi是信号相关的,Ni是信号不相关的。
以上证明了噪声模型的数学实现性,真正应用的噪声模型比上述基本模型要复杂一些。有了噪声的数学模型,就可以用统计学的方法,针对这两种不同的噪声模型进行处理。
具体的过程如下:
1> 先得到一个sensor的噪声profile(标准差 对 亮度)
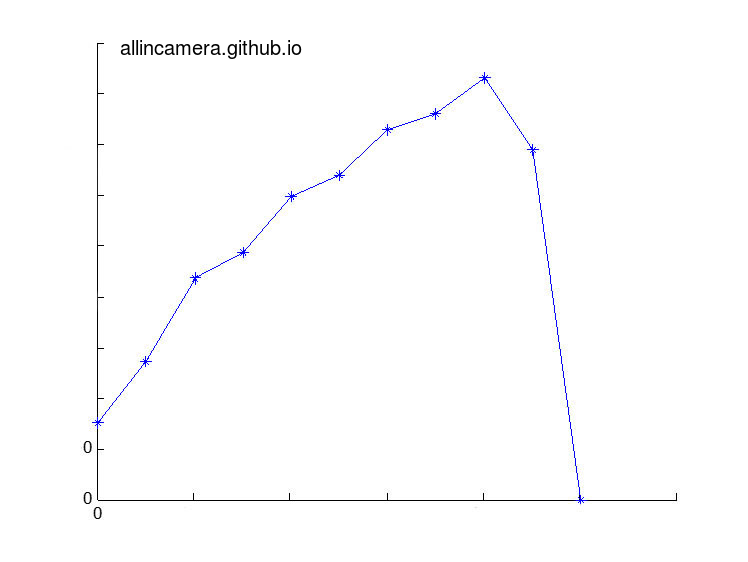
2> 利用之前说的泊松-高斯模型做curve fitting
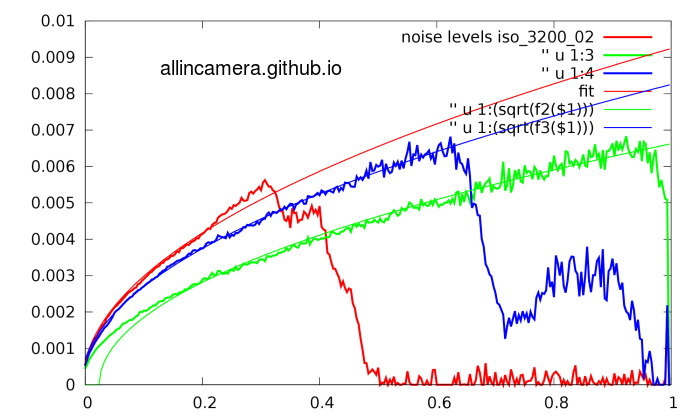
RGB三个通道有三个不同的响应,三个不同的fitting曲线。
3> Variance Stabilization
在噪声建模的论文中都用这个词Stabilization–稳定化。实际上我的理解就是把噪声对亮度做‘归一化’。因为在现在的信号处理方法中,信号依赖性的噪声处理起来非常不便。所以需要把噪声对亮度做归一化。这样就需要根据前边的fitting curve产生conversion function curve。
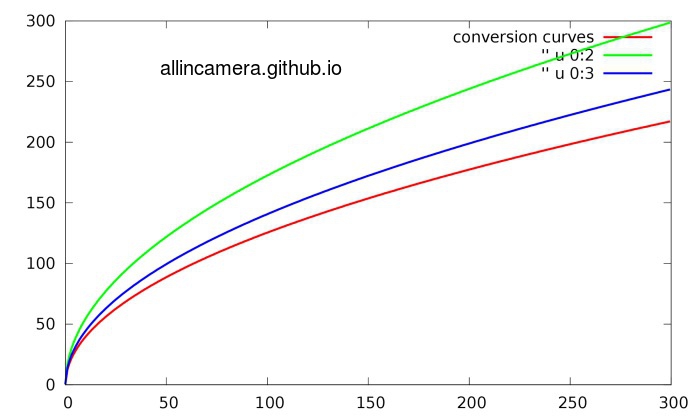
4> 把conversion function curve 作用到原始信号就会得到噪声归一化的信号:
5> 用常用的去噪方法,比如wiener filter and dct, bm3d, wavelet-based 方法, nlmeans 进行去噪
6> 做完去噪,再做反变换,就可以恢复成原始的信号
参考文献:
markku makitalo, alessandro foi: optimal inversion of the generalized anscombe transformation for poisson-gaussian noise, ieee trans. image process
alessandro foi et al.: practical poissonian-gaussian noise modeling and fitting for single-image raw-data, ieee trans. image process. vol. 17, no. 10, 2008.
k. dabov, a. foi, v. katkovnik, and k. egiazarian: image denoising with block-matching and 3d filtering. proc. spie electronic imaging, 2006.
Alessandro Foi是芬兰Tampere大学研究图像去噪和噪声建模的教授,他的文章谈到的方法很多都已经在手机camera中得到了应用,具有很高的参考价值。
本文系微信公众号『大话成像』,知乎专栏『All in Camera』原创文章,转载请注明出处。
Apr 30, 2016 · 1 minute read · Comments
hardwaresoftwaresystem
本文系微信公众号『大话成像』,知乎专栏『all in camera』原创文章,转载请注明出处并保留本声明
目前主流的双摄像头的功能。主要可以分为两大类:
利用双摄像头产生立体视觉,获得影像的景深。以及利用将不同的景深进行3D建模,图像处理,物体分割,物体识别和跟踪,对焦辅助之类的功能
利用左右两张不同的图片信息进行融合,以期望得到更高的分辨率,更好的色彩,动态范围等更好的图像质量。
这两类双摄像头功能对于摄像头的硬件有着不同的要求,前者要求两个摄像头得到像差尽量大,这样能够得到的景深精度更高,因此前者的硬件希望两个摄像头间的距离比较远才好。而后者希望两个摄像头的像在空间和时间上都尽量能够接近,因此在硬件设计的时候希望两个摄像头离得比较近。这样在两个图像融合的时候才不会因为相差产生更多的错误。
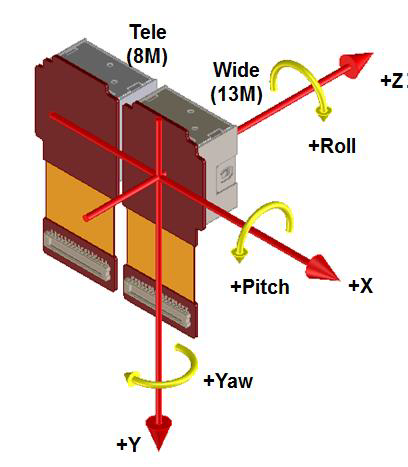
但是由于摄像头无法做的完全一致。因此无论是这两类功能的哪一类,算法都希望能在得到图像的同时,能够更多的得到硬件的实际情况如:姿势差和两个摄像头的镜头畸变等。而这些信息需要平台算法和模组生产手机生产使用相同且方便于工程化的算法进行计算,很多牵扯到硬件本身的特性,不是简单从理论计算就能解决的。以后有时间我们会继续讨论这个话题。总之双摄像头的使用过程中算法和硬件本身结合的十分紧密,不可分割。因此说到双摄像头现在首先应该关注的应该是双摄像头能带来什么样的用户体验。双摄像头中对软件硬件结合的要求远比单摄像头要高。而我们在看到一款使用双摄像头的手机的时候从它的硬件设计就能看出它是偏重于哪一类功能。下图就是常见的两个摄像头在姿势差上面的信息。就是针对3D坐标轴XYZ的平移和旋转。后面面我们把双摄像头的能实现功能给大家介绍。
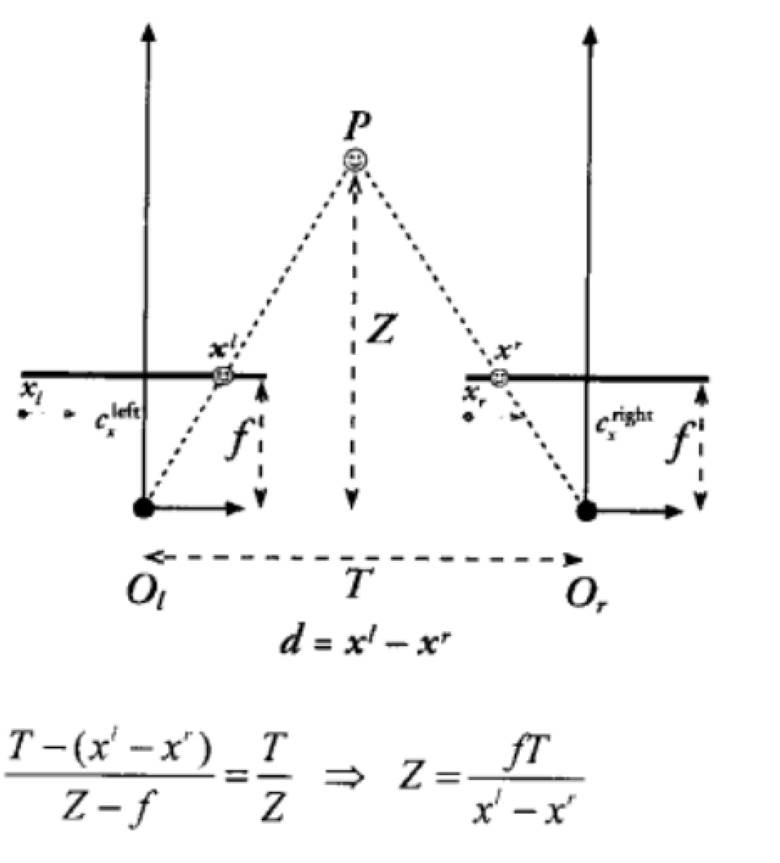
景深应用
第一类功能首先要获得当前场景的景深图。其基本原理就是基于三角定位。
背景虚化
第一类功能中最典型的就是背景虚化,在景深图的基础上将不同距离的物体进行虚化,模拟大光圈相机拍摄效果。
该功能在以前的双camera中经常能见到,如HTC的后置双摄和联想前置双摄S1。

物体分割
目前在手机上主要用于图片的裁减,和背景替换,利用景深信息可以更好的可以将不同景深的物体分割开。

3D扫描
通过不同角度下的景深图进行建模。这对景深图和算法的要求比较高。手机上的双camera之间的距离有限往往能够得到的景深图的精度不够好,景深信息处理算法复杂在手机硬件上计算的时间长,因此目前这个功能在手机上面基本没有。

目标物体距离计算和快速对焦
利用三角定位计算景深的最简单的应用

3D视频及照片制作
不同于一般的3D电影的拍摄。手机上的两个摄像头无法在图像的拍摄过程中就产生足够的视觉差,这是由于两个摄像头中间的距离和人眼不一样。而且为了能够让人们更明显的得到3D视觉效果。所以往往需要算法进行增强。

AR增强和动作识别
主要是利用两个摄像头进行手势或者姿势的识别。目前在市场上比较常见的就是leap motion 还有微软的 Kinect 都是类似的功能。亚马逊fire phone 曾经尝试在手机上实现类似的功能,但是最终手机的供电以及空间并没有给用户良好的体验。

图像合成
第二类功能都是通过将不同的图片中的不同的信息,合成到一张图片中,使合成之后的图片得到更好的效果。此类应用硬件设计中就会注意如何分别提供不同的信息。
超分辨率
主要是利用多张图片中在高频部分不同的内容生成一张清晰的图片,双camera可以通过两张照片中不同的信息进行最后的增强。
然而传统算法生成需要的图片一般都是需要更多的图片,两张图片能够提供的不同信息还是太少,如华为的Mate6 plus号称是两颗8M可以合成13M的图像,但是实际拍摄的图像的解析力还只是8M的水平,和我们自己缩放一张图片并没有什么区别。
有关解析力的区别可参阅往期解析力测试相关内容

HDR
对两个Camera设置不同的曝光参数以得到不同曝光参数的图像进行HDR合成。
以往这个功能需要通过以往一个摄像头去修改曝光时间来得到不同曝光情况下的图片,但是这种办法需要的时间长。这不仅导致了用户体验变差,且如果场景中有运动物体或者相机有移动的话会导致鬼影的问题。利用双camera则能避免类似的问题。但是大多数合成的过程中多数的HDR算法主要关注于亮度信息,多数的算法在颜色方面会有些失真。

低光提亮和去噪
低光提亮和去噪在算法上和HDR基本没有区别。主要是利用两颗摄像头中一颗黑白摄像头的低光下响应较好噪声较小的特性。
其优点是对于彩噪有不错的抑制性一般能够3个DB左右的SNR提高,但是实际拍摄的图片多数情况下效果提升有限,和有些在低光下做过特殊处理和tuning的单camera系统比并没有很明显的优势。
华为P9这一次主要就采用了这种camera的设计,从多数我们看到的网上的评价来看目前在低光下的效果有改进但并不惊艳。在华为P9之前,奇酷也采用类似的硬件设计实现这个功能。
这个功能目前看给用户的提升很有限,也许后面还有挖掘的潜力。

光学变焦
最近比较好的应用趋势是利用一颗正常的FOV的摄像头模组和一颗远焦镜头的模组达到光学变焦的效果。
从苹果收购以色列的Linx公司还有苹果公司最新公布的专利来看,水果公司最新的专利来看这个功能很可能是水果公司的双camera的主要功能。远焦镜头的视场角要比正常的镜头小很多,但是相同距离下图片的解析力也会高不少。利用远焦镜头可以提供的较好的分辨率既可以在平时拍照的时候利用融合算法提高中心区域的分辨率,也可以在变焦时利用远焦的照片提高ZOOM后的解析力。从之前看到过的另外一家以色列公司CP的算法效果来看,如果手机上实现的好的话可能在中心区域超过现有手机摄像头最大的解析力,在效果上和光学zoom相差不大。虽然这个功能在硬件设计的时候有着远焦模组过高的问题,但是这依然是第二类功能中目前能看到效果最好的功能。

现状总结
从目前市面上能看到双Camera手机来看:
偏景深类功能的手机目前主要的问题是景深信息不够准确计算速度慢。无法实时得到景深信息。不过目前手机硬件的发展速度很快,很多ISP的设计已经开始考虑双camera的实时景深。今年很多实时景深的ISP将开始在平台端普及,虽然分辨率还不是很理想。但是随着实时景深的普及,景深信息的分辨率的增加,相信后面利用景深信息实现的场景物体识别类的功能相信会越来越多。类似我们之前看电影中的一些现实增强的效果我相信 也会越来越多。而且这类功能在智能机器人领域也是目前的热门。如陪李总理的打球的机械人就是这类功能的延伸。不过进入平常百姓家这个肯定需要时间。
而偏第二类图片融合得到更好图像质量的功能,从目前已有的手机来看都不是很成功。不过实现光学变焦的效果从算法效果的层面上来看效果很不错,或许苹果的双摄出来之后能在这个领域带起一个风潮。
两类应用对摄像头模组要求是不同的,前者要求模组间的距离较大为好,后者则要求模组间的距离尽量小。虽然无论做的多小但由于模组本身的尺寸,两个摄像头间肯定会有些距离的。比如华为P9两个摄像头间的距离已经小于1厘米,但是再想做的更小可能需要突破性的设计。
当然,为其中一类功能设计的双摄像头模组也可以实现另外一类功能,只是勉强实现会增加算法的复杂程度,在最终实现的效果上也会受到很大制约。比如P9虽然也实现了景深功能但效果和专门为景深功能功能设计的双摄像头比还是很有差距的。
双摄像头的风潮刚刚开始,后续我们会邀请不同领域的专家来介绍双摄像头实现的一些具体问题。
本文系微信公众号『大话成像』,知乎专栏『all in camera』原创文章,转载请注明出处并保留本声明
Apr 29, 2016 · 1 minute read · Comments
software
本文系微信公众号《大话成像》,知乎专栏《大话成像 all in camera》原创文章,转载请注明出处。
上一篇讲过了temporal noise和Fix patter noise的分离,通过多帧平均可以去除掉temporal noise,并分离出FPN,在这篇将介绍如何去除FPN。
在信号处理教科书中,介绍过很多经典的图像去噪方法,主要的是针对随机噪声的,对于图像中非随机噪声,比如sensor本身的物理缺陷导致的hot pixel,weak pixel 或是dead pixel,一般称之为impulse noise,对于impulse noise有单独的处理方法,因为他们不属于随机噪声。
随机噪声也就是在比图像的真实信号或高或低的不确定变化。
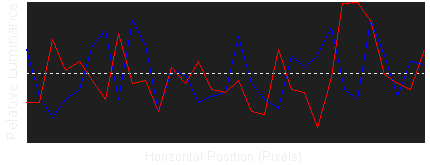
如果中间的虚线视作真实信号,红色和蓝色的曲线代表随机噪声叠加后的信号,如果虚线定义为0,那么所有随机噪声求和应为0 ,在统计学上叫零和噪声。由于零和噪声的这种特点,均值滤波可以降低图像的噪声。
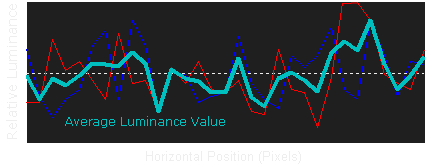
如图所示,浅蓝色的线代表红蓝线求均值以后的信号,波动的幅度明显减小了,也就是噪声降低了。
均值滤波与变换域去噪
教科书里讲图像去噪声,第一个提到的就是均值滤波,在图像处理中,就是当前像素的值用周围n个像素的均值来代替。
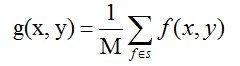
在实际信号处理中,就是用一个n x n 的模版 A 对图像进行卷积,比如:
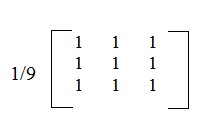
当前像素就是处在矩阵中心的像素,它的值等于周围所有像素的值包括它自身取均值。
这样的一个基本均值滤波,它可以去掉噪声,但同时也会把图像搞模糊,比如当前的像素正好是一个图案的边缘,左边是白色的,像素值是200,右边是黑色的,像素值是10,做完均值滤波,(200+200+200+10+10+10+10+10+10)/9 = 74, 这样图像的细节就被模糊掉了。于是人们就对这种均值滤波进行了一些改进,比如增加图像边缘方向的判断,红线的方向上相邻像素的数值差不多,所以在做均值的时候只把这个方向的两个像素计算在内。这样既去掉了一些噪声,又保持了锐度。
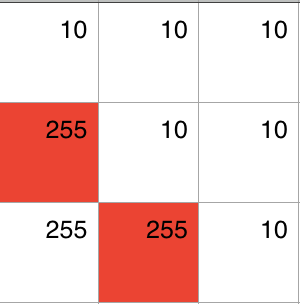
这样由于做均值的像素变少了,去噪的效果不太好,于是有人想出一种none local mean的方法,也就是做均值的像素不再是领域的像素,扩大些范围找相似的,然后再做均值。

绿色的部分和中心要处理的部分很相似,求均值的时候就把这些部分算进去,而红色的部分不相似,去均值的时候就排除这些部分。很容易想象,搜索的范围越大,计算量越大。
这些方法都是从空间的角度去思考如何去噪,也就是所谓的spatial noise reduction,这条路子能想的方法也都做得差不多了,于是有人换个角度想问题,就有了变换域做去噪的方法。通过数学变换,在变换域上把信号和噪声分离,然后把噪声过滤掉,剩下的就是信号。如下图,
没有噪声的信号看起来比较光滑:

带噪声的信号就会有些毛刺:
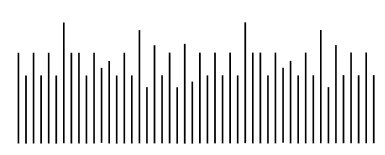
把带噪声的信号变换到一个域(比如频域,小波域等等)

高于一个阈值的部分就是噪声,设一个截止值,把高于截止值的部分去掉
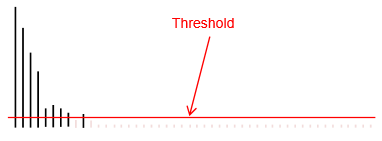
再做反变换,就得到了干净的信号。

从频率上可以把噪声分为高中低频噪声,用这种变换域的方法就可以把不同频率的噪声分离,然后有效的去掉。像傅立叶变换,小波变换都是比较常见的变换域方法。
BM3D去噪
简单来说,BM3D融合了spatial denoise和tranform denoise,可以得到最高的峰值信噪比。它先吸取了NLM中的计算相似块的方法,然后又融合了小波变换域去噪的方法。这是芬兰Tampere工业大学在2007年发表的论文里提出的算法。(了解NOKIA的人就知道Tampere这个城市就是NOKIA最早起源的地方)。
具体算法如下:
第一步,搜索相似块,然后把相似的块grouping成一个个3D stack。(图像本身是2D,变成stack就成了3D)
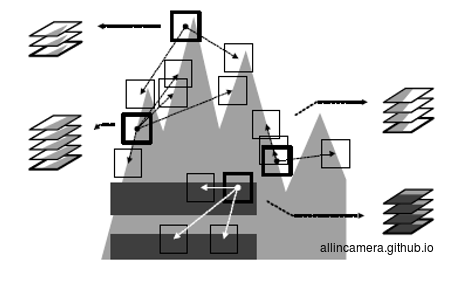
第二步,把这些3D stack进行变换域

第三步,3D 协同滤波—-听着很邪乎,细节需要自行wiki
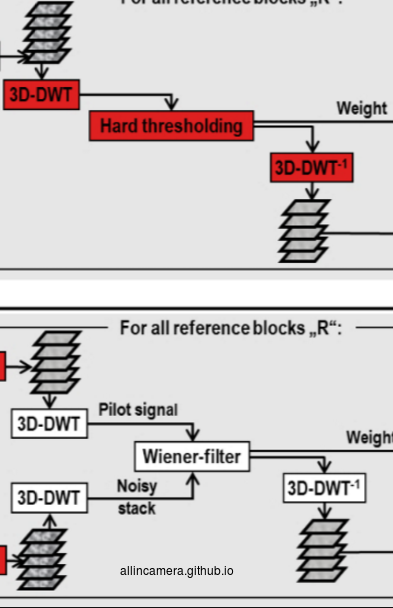
第四步,反变换以及blending

红色模块里提到的在变换域中thresholding的设定,有自适应计算的方法,但在工程中用的效果比较好的是噪声模型法,关于噪声模型,我们会在下一篇中进行介绍。
本文系微信公众号《大话成像》,知乎专栏《大话成像 all in camera》原创文章,转载请注明出处。
Apr 19, 2016 · 2 minute read · Comments
software
本文系微信公众号《大话成像》,知乎专栏《大话成像 all in camera》原创文章,转载请注明出处。
噪声分类
噪声有很多种分类方法,比如从频率上分,可以分为高频,中频,低频噪声。




从色彩空间上分,可以分为luma noise亮度噪声与chroma noise彩色噪声。

从时态上分,可以分为fix pattern noise与temporal noise。Fix pattern noise 与时间无关,表现上看就是噪声幅度不随时间变化。Temporal noise是随时间变化,在低光下录制的视频中不断变化的细小信号就是temporal noise。
也有的分法把fix pattern noise定义为在图像行或者列存在的一条条的噪声,如下图所示。

Temporal noise视觉上是一种高频噪声。
噪声计算
均值 $\mu = \dfrac {\sum^{n}_{i=1}X_{i}}{n}$
标准差 $\sigma=\dfrac {1}{n-1}\sum ^{n}_{i=1}\left(u-x{i}\right)^{2}$
图像的标准差可以作为图像噪声水平的评价值。
按照如下曝光时间,每个曝光时间拍30张black 照片。
exp_time = [0.063, 1.003,16, 64,257,513,770,1027,1283,1540,1797,2054];
raw_avg = 0;
for kk = 0:30:(30*12-1)
for i = 1:30
fname = fileNames{kk+i};
fprintf('processing %s %d\n', fname, kk+i);
raw = double(imread([fold fname]));
raw = raw(:,:,1);
raw_avg = raw + raw_avg;
end
raw_avg = raw_avg./30;
avg_signal((kk/30)+1) = round(mean2(raw_avg));
fpn_total((kk/30)+1) = std2(raw_avg);
fpn_col_exp((kk/30)+1) = std(mean(raw_avg,1));
% avg_sig_col_exp((kk/30)+1,:) = mean(raw_avg,1);
fpn_row_exp((kk/30)+1) = std(mean(raw_avg,2)');
% avg_sig_row_exp((kk/30)+1) = mean(raw_avg,2)';
如上计算,可以得到图像的平均信号,每个曝光的FPN noise,以及行,列FPN noise,行列均值。
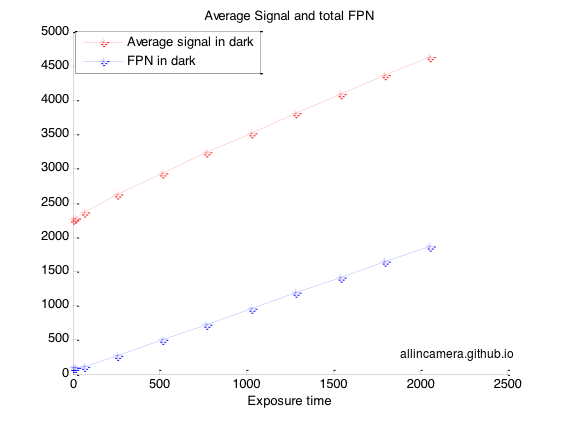
把曝光逐渐增加,确保图像能够达到饱和,在10个曝光值,每个曝光值下拍30张flat field照片
raw_avg = 0;
temp_noise = zeros(30,480*752);
for kk = 0:30:(30*11-1)
for i = 1:30
fname = fileNames{kk+i};
fprintf('processing %s %d\n', fname, kk+i);
raw = double(imread([fold fname]));
raw = raw(:,:,1);
raw_avg = raw + raw_avg;
temp_noise(i,:) = raw(:)';
end
raw_avg = raw_avg./30;
std_temp_noise = std(temp_noise,1);
avg_signal((kk/30)+1) = round(mean2(raw_avg));
temporal_total((kk/30)+1) = median(std_temp_noise);
如上计算,可以得到图像的temporal noise
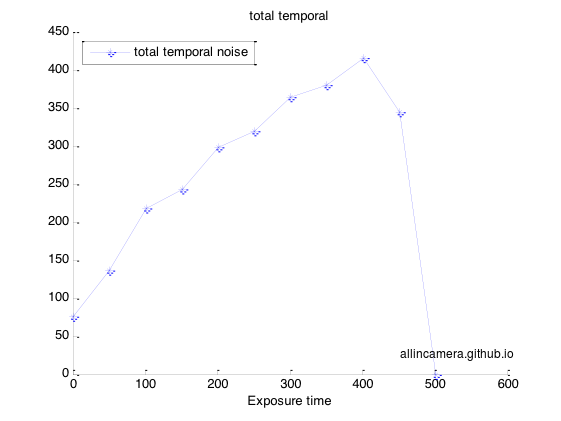
最后图像饱和,所以噪声降低至0。
FPN noise是相关噪声,temporal noise是不相关噪声。
两个图像相加:
$S = S_1 + S_2$ S代表信号
$\sigma^{2}_{t}=\sigma^{2}_{t1}+\sigma^{2}_{t2}$ $\sigma_{t}$ 代表temporal noise
信噪比SNR $\dfrac {S}{\sigma_{t}}=\dfrac {S_{1}+S_{2}}{\left(\sigma^{2}_{t1}+\sigma^{2}_{t2}\right)^{0.5}}$
当 $S_{1} = S_{2}$ , $\sigma_{t1} = \sigma_{t2}$, 信噪比SNR $\dfrac {S}{\sigma_{t}}=2^{0.5}\dfrac{S_{1}}{\sigma_{t1}}$
当 $S_{1} = S_{2}=...=S_{n}$ , 信噪比SNR $\dfrac {S}{\sigma_{t}}=n^{0.5}\dfrac{S_{1}}{\sigma_{t1}}$
该公式从理论上证明了n帧平均会降低temporal noise $n^{0.5}$ 倍。所以信号处理中去除temporal noise的方法就是多帧平均加运动检测,如果存在图像存在变化就不累加,如果图像无变化就累加平均。
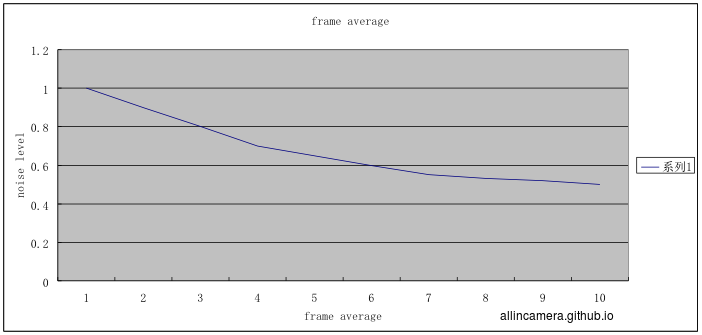
而FPN noise 是相关噪声
$\sigma_{fpn} = \sigma_{fpn1} + \sigma_{fpn2}$
$S = S_{1} + S_{2}$
$ \dfrac {S}{\sigma_{fpn}} = \dfrac {S_{1}+S_{2}}{\sigma_{fpn1}+\sigma_{fpn2}} $
当 $ S_{1} = S_{2} $, $ \sigma_{fpn1} = \sigma_{fpn2} $ 时, $ \dfrac {S}{\sigma_{fpn}} = \dfrac {S_{1}}{\sigma_{fpn1}} $
多帧平均不会降低FPN。
通过上图可以看出,经过多帧平均后,噪声的floor变成了FPN。
通过多帧平均可以分离temporal noise和FPN,然后用其他信号处理的方法去除FPN,下一篇将介绍去噪的Spacial domain 和 transform domain的方法。
Apr 7, 2016 · 1 minute read · Comments
hardwaresoftwaresystem
当前手机成像系统中普遍使用反差式对焦系统,也就是计算当前图像的锐度,依照图像锐度与镜头位置的关系,寻找最锐度最高的镜头位置作为合焦位置的方法。在搜索策略上各厂商基本相似,在锐度提取也就是清晰度的计算上,应该根据光学特性的不同做差异化设计。
基于芯片硬件设计的方便性考虑,大部分的锐度评价函数都设计为一个m x n算子,记作P,算子的填充决定其特性:一般是高通,或者是带通滤波器。如果图像记作G,那么图像的锐度S可以表示为:
S = P * G P 对 G 做卷积。
高通与带通滤波器的优缺点
高通滤波器对高频成分很敏感,当成像系统离焦不远时,图像高频成分很容易被提取出来,随着镜头的移动,计算出锐度的差异很明显。但是当图像离焦很远时,比如对焦的物体消失,背景物体又在远处,高通滤波器对图像的响应就不明显,这样镜头移动计算出的锐度变化就不明显,造成搜索失败。
如下图
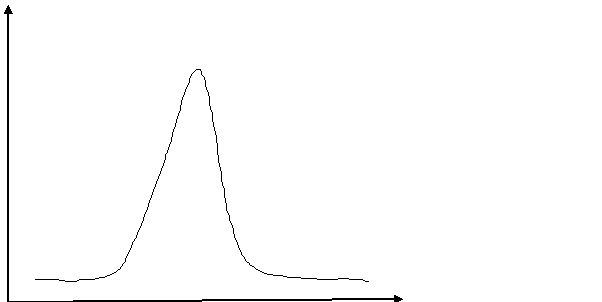
当锐度值在曲线两侧,无论镜头如何移动,变化都非常不明显,这样搜索算法就很难工作,这个评价函数就是不合适的。为了解决这个问题,就需要在设计滤波器P的时候,让低频成分多通过一些。
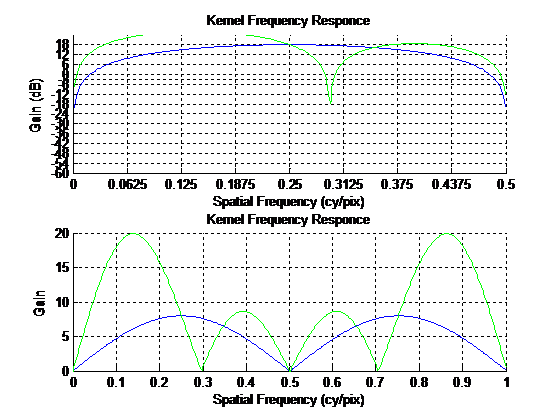
蓝色的曲线是滤波器P1的频率响应,绿色的曲线是滤波器P2的频率响应,相比可见,绿色曲线可以让更多低频成分通过。
选择一个滤波器后,需要根据实际图像进行计算仿真,画出这个滤波器对不同离焦程度图像卷积所产生的锐度值
kern = [-1 -2 -3 -5 -8;8 5 3 2 1];%c
% kern = [-1 0 1; -2 0 2; -1 0 1];%r
% kern = [ -1 -1 -1;-1 0 1;1 1 1];%g
% kern = [ -1 -1 -1;-1 8 -1;-1 -1 -1];%b
% kern = [ 7 5 -1 0 -1 ;1 0 -5 1 -7]; %m
kern = [ 6 0 6 0 0 ;0 -12 0 0 0];%k
% kern = [-5 -4 0 4 5;-8 -10 0 10 8;10 -20 0 20 0;-8 -10 0 10 8;-5 -4 0 4 5]%y
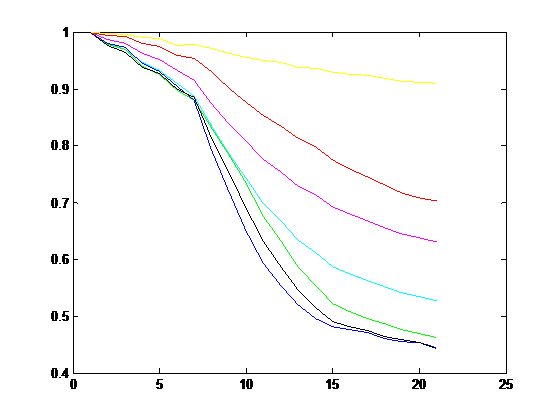
上图就是上面的各个滤波器的仿真结果,横坐标是离焦程度,从0到25,离焦程度逐步变大。纵坐标是计算出的锐度值,1表示最大。通过这个曲线,可以看出对不同离焦程度图像滤波器的响应,依据响应曲线的特点进行选择。
Apr 7, 2016 · 1 minute read · Comments
hardwaresoftwaresystem
相差式自动对焦与反差式自动对焦是现在手机成像系统中两大主要自动对焦方式。相比反差式自动对焦,相差式自动对焦只需要一次计算,就可以完成对焦。
当前比较流行的是片上相差自动对焦(on chip phase detection autofocus), 在生产sensor的时候,把某些用于相位检测像素遮住左边一半或者右边一半,如下图

上图只是示意图,各个厂商的半掩模的工艺各有不同,在对IR filter或者microlens的处理上也不相同,但是基本的原理都是让图像形成左右两幅类似人眼的不同光学通路的图像。
这样左右侧的相位检测像素就会产生这样的图像:
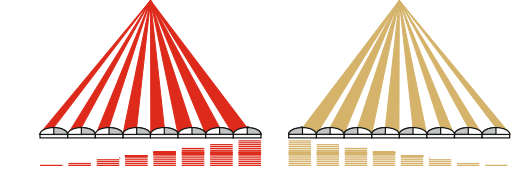
数字化以后就产生了两个序列。
图像聚焦时,两个序列做互相关运算产生的数值变小,图像离焦时,两个序列做互相关产生的数值变大。如果对相机模组进行校准—-针对一个固定图形的高频图像移动镜头,计算互相关运算产生的数值,记录下来成为基准表。在相机工作时,根据实时计算的互相关数值,通过查找基准表,就可以知道当前的离焦程度,从而找到移动方向和移动到什么位置。
数学推导简化起来就是如下公式:
左右两个图像产生的数列做互相关,得到一个对焦函数,可以把相差与镜头的偏移量变成一一对应关系。
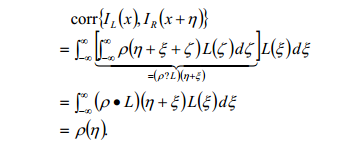
实际工程上计算得到的结果就如下边图中所示,5x5窗口,每个窗口里边的统计数据包括两个部分,高16位是相位差,低16位是置信度。在平坦区域,置信度低,在细节丰富的区域,置信度高(300)。

通过固定图卡校准可以得到lens 偏移量和相差的对应数组:
PDAF_Calibration[][2] = {{1,1},{2,3},{3,5},{4,7},{5,9},{6,10},{7,11},{8,12},{9,13},{10,14},{11,15},{12,16},{13,17},{14,18},{15,19},{16,20}, {20,30},{24,40},{28,47},{32,50},{40,70},{48,80},{56,96},{64,110},{80,138},{96,160},{112,180},{128,210}};
所以当AF开始工作时,通过实时计算得到相差值,eg: 210, 那么对应移动lens的距离,就是128,如果得到相差值是-210,就移动lens向反方向128个单位。
Apr 6, 2016 · 1 minute read · Comments
hardwaresoftwaresystem
上一篇也说到MTF曲线的时候横坐标是空间频率。一般使用黑白交替的线对来表示空间频率。而空间频率的单位一般是线对每毫米(lp/mm),周期每毫米(cycles/mm),周期每像素(cycles/pixel),线宽每图像高(LW/PH Line Widths per Picture Height),线对每图像高(lp/ph)。其中lp/mm是目前使用最多的单位。cycles/pixel是在数码相机中的成像系统的。数码相机下一个像素就是1 cycles/pixel,两个像素就是0.5 cycles/pixel,4个像素是0.25 cycles/pixel.其它单位的计算如下,纵向是已知横向是未知。
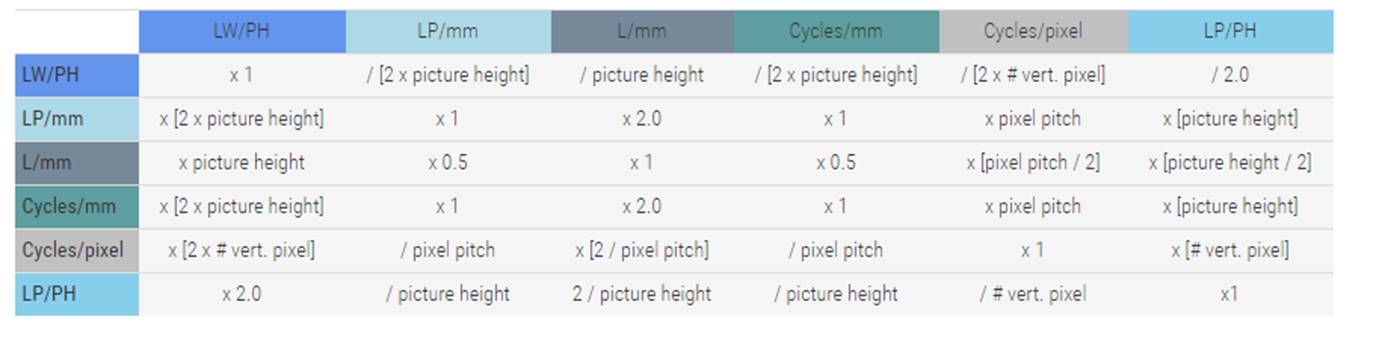
当知道了空间频率的单位之后又有了一个问题。到底用什么样的空间频率去评价MTF合适呢?这个时候经常能看到一个名词奈奎斯特(Nyquist)频率,这是来自采样定律。奈奎斯特和成像有什么关系呢?
数字相机的Sensor在成像过程中就相当与对镜头成的模拟像进行空间数字采样。
奈奎斯特采样定理是指在进行模拟与数字信号的转换过程中,当采样频率大于信号中最高频率的2倍时,采样之后的数字信号完整地保留了原始信号中的信息,但是一般实际应用中保证采样频率为信号最高频率的5~10倍。数码相机的Nyquist取决于pixel 的大小.根据前面给出的空间频率单位转换公式。
对于给定的Pixel size的sensor
Nyquist 频率= 1000[µm]/(pixel_pitch [µm]X2)
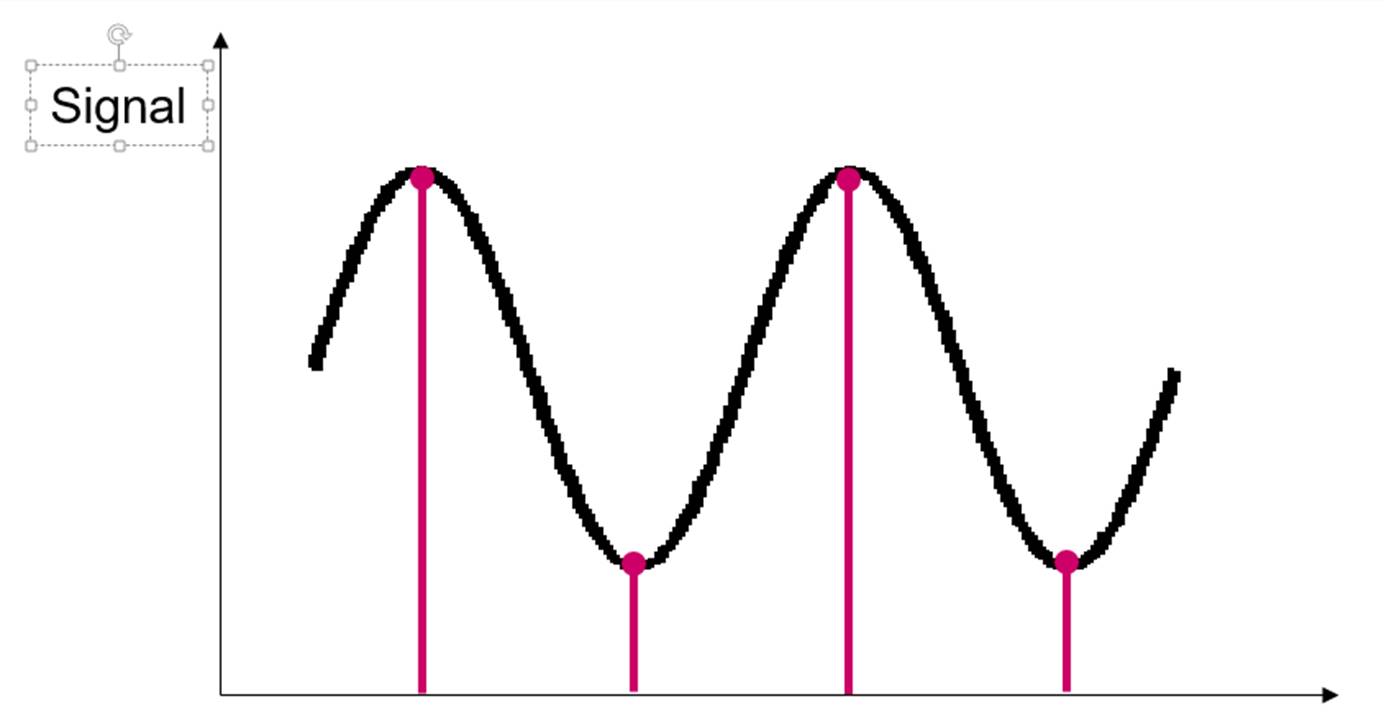
评价MTF使用的奈奎斯特频率(Nyquist频率)是离散信号系统采样频率的一半,也就是一个方向上的像素数一半。采样定理指出,只要离散系统的奈奎斯特频率高于被采样信号的最高频率或带宽,就可以避免混叠现象。但这只是理论上。我们先看下一个接近奈奎斯特频率的频率的采样过程。当然下面的成像过程都是基于一个理想的没有MTF衰减的镜头的情况下。我们实际的像素对正弦图卡的采样过程可以模拟为

而在采样理论中的采样过程中类似下图。两个采样点之间的周器和数字成像系统的像素一样。但是希望采样点能够尽量小。

采样定理中的只要小于奈奎斯特频率频率都可以被采样还原是有两个条件的。
1采样点的尽量小,而我们的像素大小实际上接近于
2重建信号的过程需要以一个低通滤波器或者带通滤波器将在奈奎斯特频率之上的高频分量全部滤除,同时还要保证原信号中频率在奈奎斯特频率以下的分量不发生畸变。
这两者在图像系统中都很难满足。因此很多时候即使采样过程中信号的最大频率小于奈奎斯特频率频率依然无法很好的得到采样还原。
即使选取一个略小于奈奎斯特频率频率的正弦图卡。当发生相差的时候像素就很有可能无法正确采样出来实际图卡的原来的形状。但是多数情况下使用理想的采样模型是可以将原有信号正确的采样出来的,下面两张图是相差的影响对实际像素的采样影响。
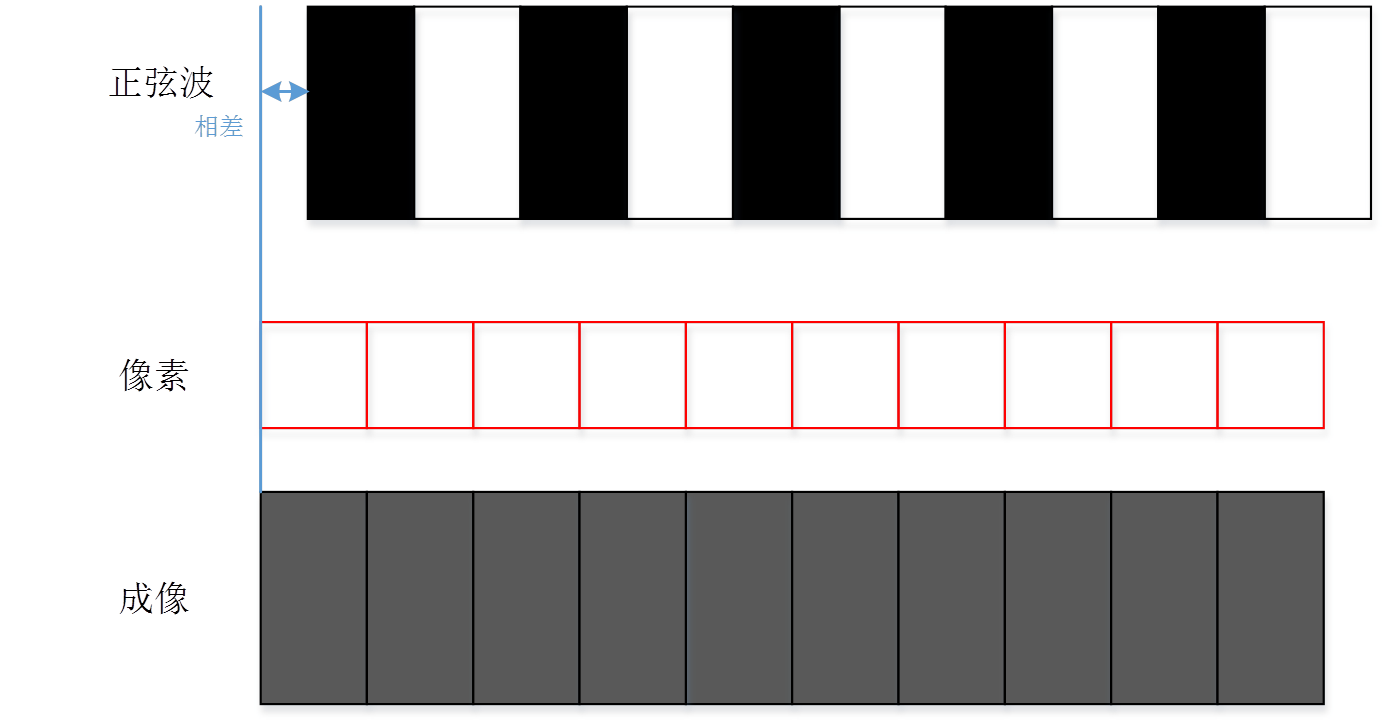

前面提到当频率高于奈奎斯特频率的时候会产生混叠现象。混叠(aliasing) 在信号也称为叠频;在成像上称为叠影,叠影会产生伪纹也就是平常说的摩尔纹。下面的就是一个高于Nyquist频率的频率产生伪纹的采样情况。

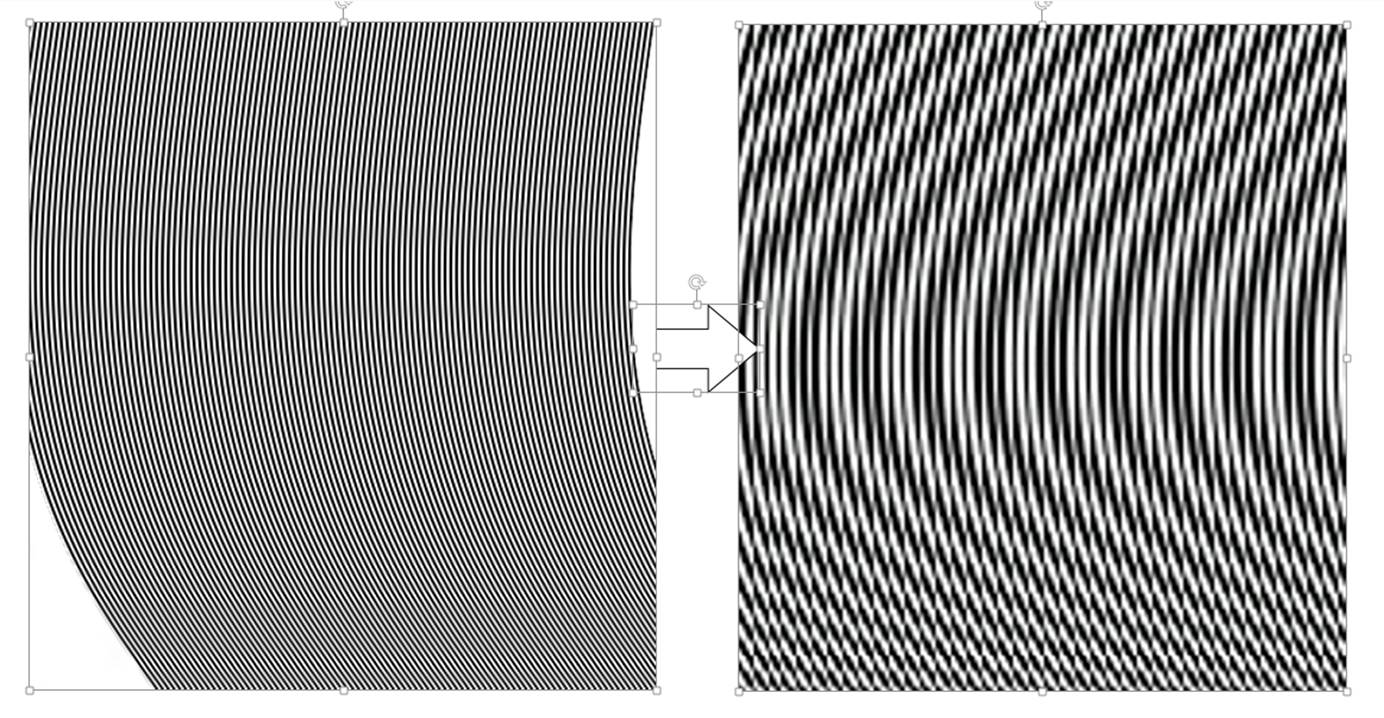
从采样的一般规律来说如果要消除上面这些相差和混叠的影响就需要提高采样的频率。对于常用的采样频率我们可以参考示波器。示波器是一个常用的采样系统,一般示波器的采样频率在被采样频率的5到8倍。但是数字成像系统不同于示波器的是采样的频率在感应器被确定了之后就已经定了。更多的我们是希望知道原有图像在什么频率下分析成像系统的品质更合适。图像采样的过程中肯定是频率越低的图像越清晰。但是一般什么频率的图像是采样的清晰度是应该可以很好的分辨呢。根据如下图一样的仿真和经验,一般能很好分辨的频率在每个线对4个像素左右,也就是1/2奈奎斯特频率.。下面两张图是在1/2 Nyquist频率采样的情况
没有相差的1/2 Nyquist频率采样的情况
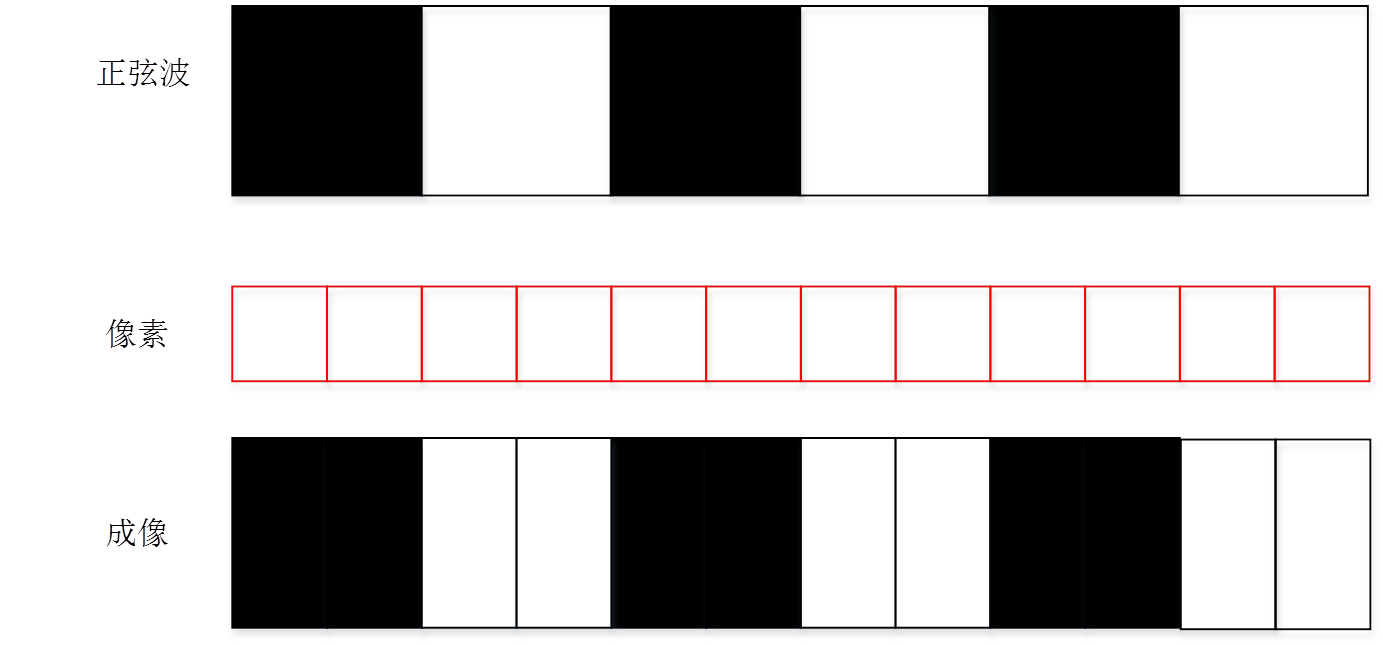
有相差的1/2 Nyquist频率采样的情况
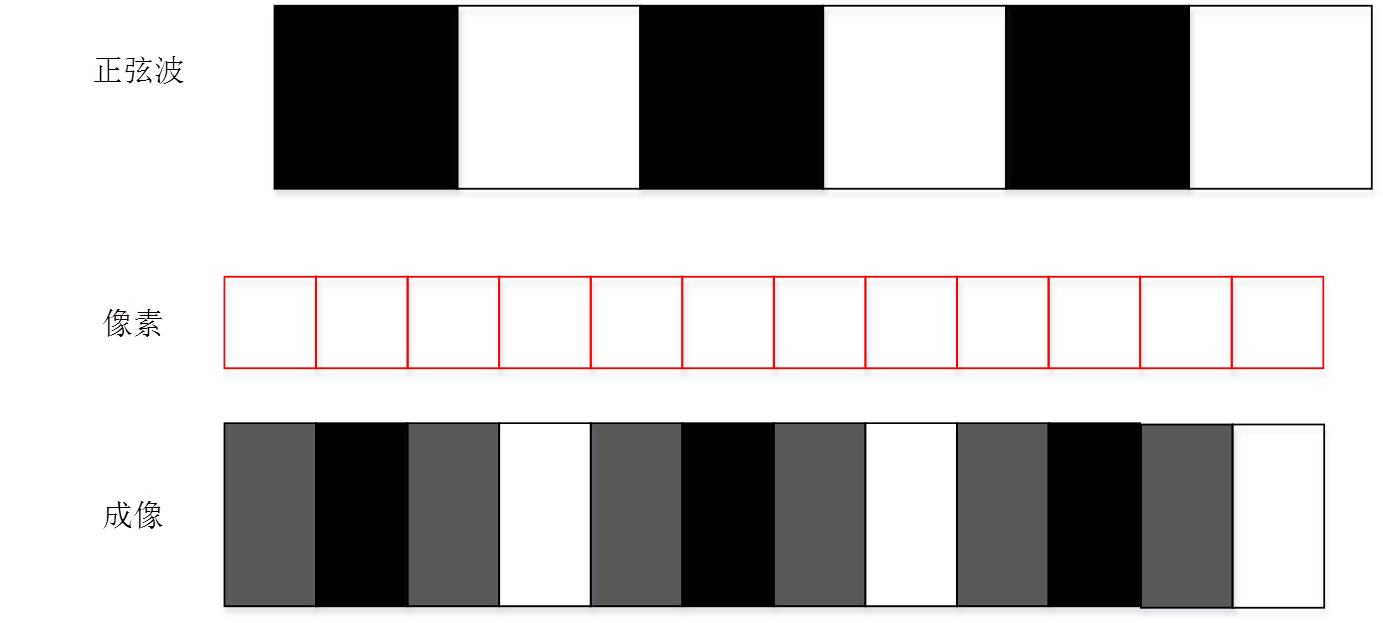
我们可以看到在1/2 Nyquist下即使有相差,也可以基本上还原原有图像的形状了。但是这只是仿真像素的采样过程中,在实际测试过程中由于镜头,噪声和测试环境影响在1/2奈奎斯特频率附近测试MTF值很不稳定。因此也经常选取更低1/4奈奎斯特频率作为MTF测试值所选取的频率。不过MTF的评价并不是简单的看一个频率就可以评价一个成像系统的效果,MTF曲线是一个整体。下一篇中将介绍怎么来通过SFR算法得到MTF曲线评价一个手机模组。
Apr 6, 2016 · 1 minute read · Comments
hardwaresoftwaresystem
基本概念
成像系统的解析力一直是摄像头最关键的指标之一。所有用户拿到一张照片的时候首先看到的是照片清楚不清楚,这里的清楚说得就是解析力。但是如何评价一个成像系统的解析力也是大家一直在探讨的问题。目前主流的办法主要有三种TV line检测,MTF检测,和SFR 检测。
TV line
TV line主要用于主观测试,也有一些读取TV line的软件如HYRes。但是总体来说没有一个具体的标准。大多数公司是以人的读取为标准。不同人的读取,以及状态的不同都会导致读取值的不稳定。而且如ISO12233 chart 实际上我们读出的线对数只能代表读出位置的状况。尤其中心的TV line跨度很大,很难反映一个成像系统
MTF
MTF是Modulation Transfer Function的英文简称,中文为调制传递函数。是指调制度随空间频率变化的函数称为调制度传递函数。个传递函数最开始是为了说明镜头的能力。在各个摄像头镜头中经常采用MTF描述镜头的MTF曲线,表明镜头的能力。这些曲线是通过理想的测试环境下尽量减少其它系统对镜头的解析力的衰减的情况下测试得出的。但是其实MTF也可以涵盖对整个成像系统的解析力评价。在这里咱们就不多讨论这个问题了,如果有兴趣可以开另外一篇文章讨论。
SFR
SFR是 spatial frequency response (SFR) 主要是用于测量随着空间频率的线条增加对单一影像的所造成影响。简言之SFR就是MTF的另外一种测试方法。这种测试方法在很大程度上精简了测试流程。SFR的最终计算是希望得到MTF曲线。SFR的计算方法和MTF虽然不同但是在结果上是基本一致的
测量方法
现在我们来看一下传统的MTF是怎么测量出来的,后面我们再针对SFR的原理和MTF的关系进行一些介绍。在以后的文章中我们在介绍一些MTF和SFR测试需要注意的问题。
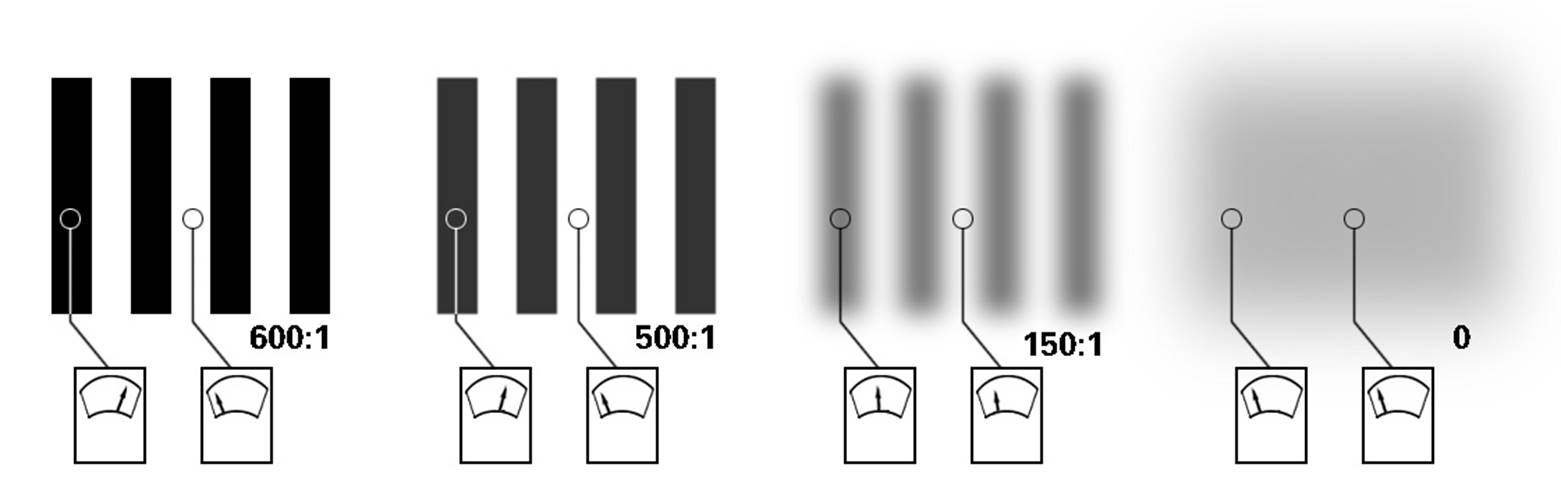
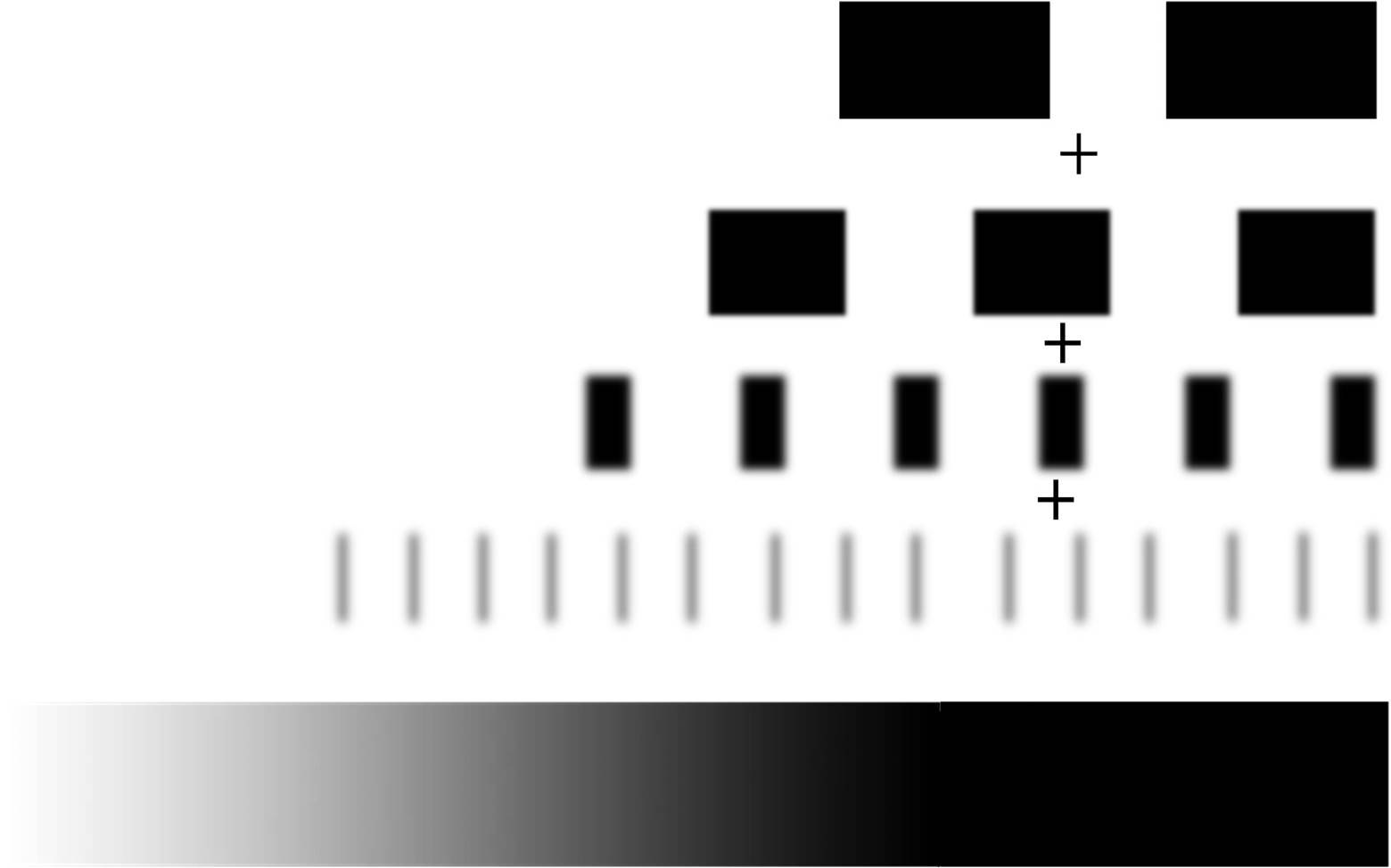
从上面我们知道MTF是描述不同空间频率下的调制函数。那么什么是空间频率呢?通常,描述频率的单位是赫兹(Hz),比如50Hz、100MHz之类的。但空间频率的表述习惯用“每毫米线对”。(LP/mm),就是每毫米的宽度内有多少线对。每两条线条之间的距离,以及线条本身的宽度之比是个定值,目前我国分辨率的标板规定,这个定为公因子是20√10≈1.122等比级数。一般MTF的计算离不开线对。下面这个图就是一张不同频率的线对测试图 ,可以看到图卡本身黑色和白色的对比是很清楚的。
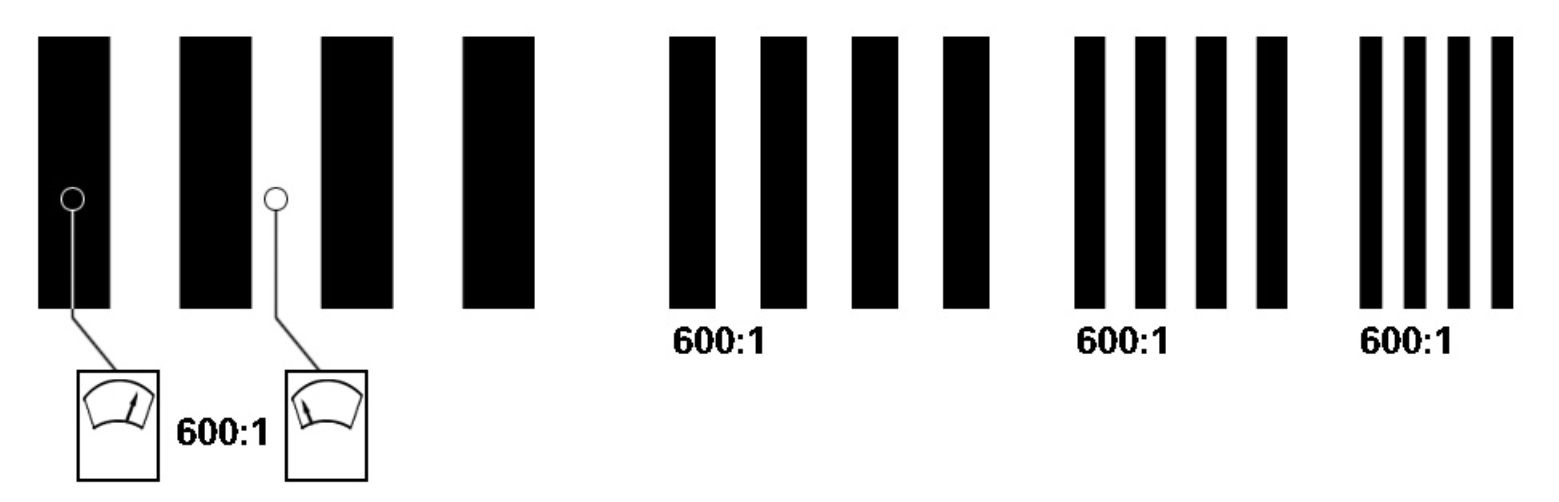
实际拍摄的时候,就像上图一样频率越高(越细)的线对就越模糊。这就是我们实际拍摄场景中到一定小的纹理的就拍摄不清楚的原因。而MTF的计算就是计算线对间最亮和最暗线对的对比度。计算公式为
MTF = (最大亮度 - 最小亮度) / (最大亮度 + 最小亮度)
所以MTF的计算不会出现大于1的情况。像下面的图表示的这样,当我们测试了很多不同频率下的MTF值。通过将这些值和空间频率进行一一的对照。通过这条曲线我们就能知道现在的成像系统在什么样的空间频率下的对比度如何。
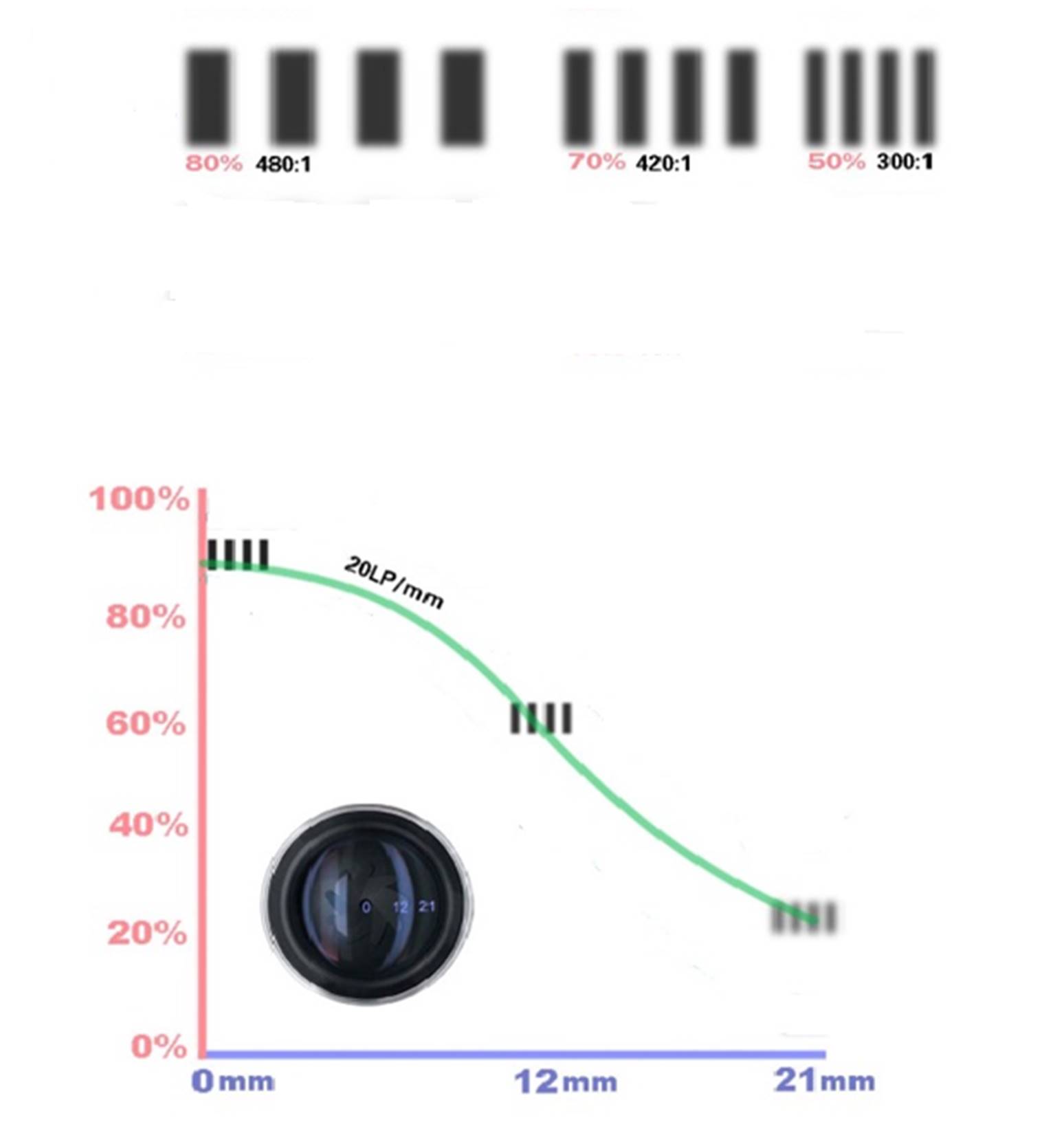
SFR是怎么测试和计算的呢。首先SFR不需要拍摄不同的空间频率下的线对。它只需要一个黑白的斜边(刀口)即可换算出约略相等于所有空间频率 下的MTF。如何通过一个斜边计算出大家可以去看下ISO12233-2000那篇文档,里面说的很详细。具体的流程如下图。
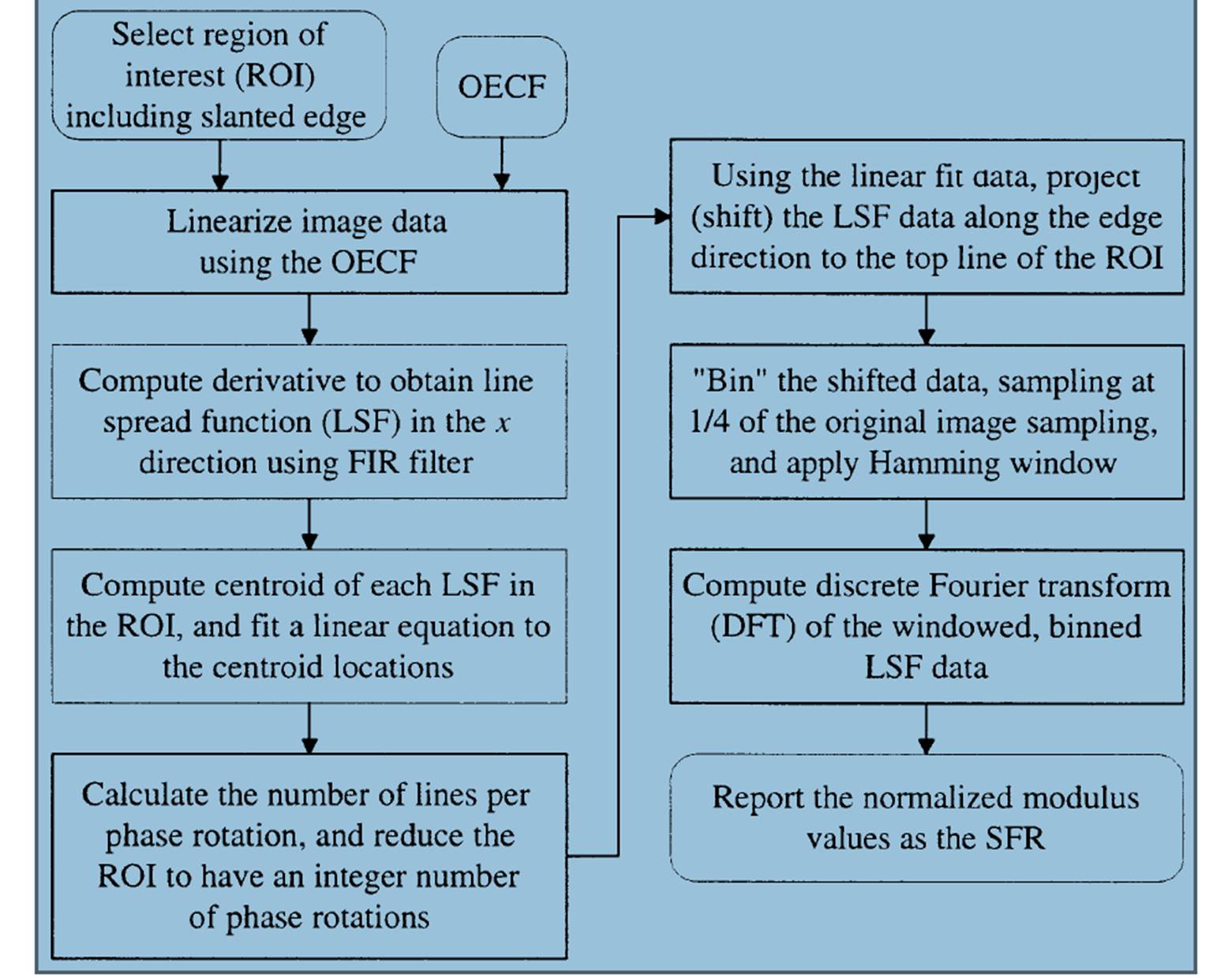
其实简单得来说呢,SFR是通过这条斜边的图进行超采样的到一条更加细腻的黑白变换的直线(ESF)。然后通过这条直线求导得到直线的变化率(LSF)。然后对将这个变化率进行FFT变换就能得到各个频率下的MTF的值。这里面的ESF,LSF,都是什么呢?
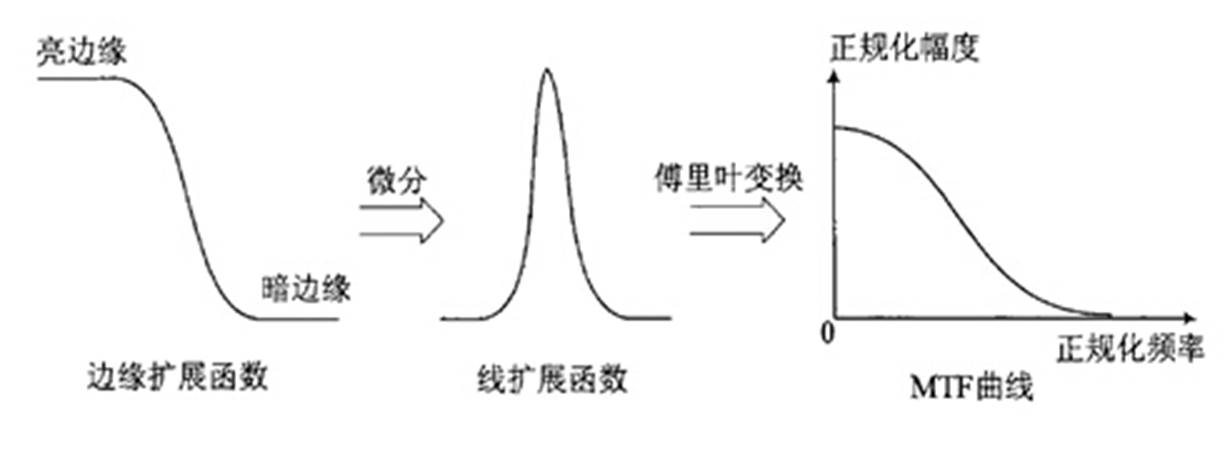
点扩展函数PSF(Point Spread Function)、线扩展函数LSF(Line Spread Function)和边缘扩展函数ESF(Edge Spread Function)是SFR 计算中的几个重要的概念。点扩展函数PSF是点光源成像后的亮度分布函数,如下图所示,用PSF(X,Y)表示。点扩展函数是中心圆对称的,通常以沿x轴的亮度分布PSF(X,Y)作为成像系统的点扩展函数。
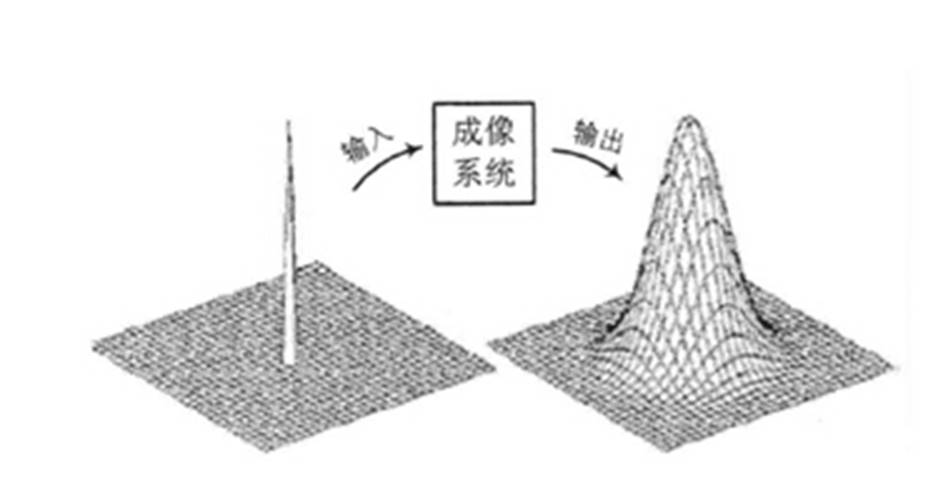
当获取点光源像的亮度分布函数PSF(X,Y)后,对其进行二维傅里叶变换即可得MTF (u,v)。因此,从理论上讲,从PSF也是获取MTF的一个方法。但是,在实际的应用中,由于地面点光源强度很弱,此方法一般较少采用。相对于PSF来说,LSF的能量得到了一定程度的加强。SFR计算MTF就通过ESF来得到LSF然后进行FFT得到MTF各个频率的值的。这几者之间的关系如下图。
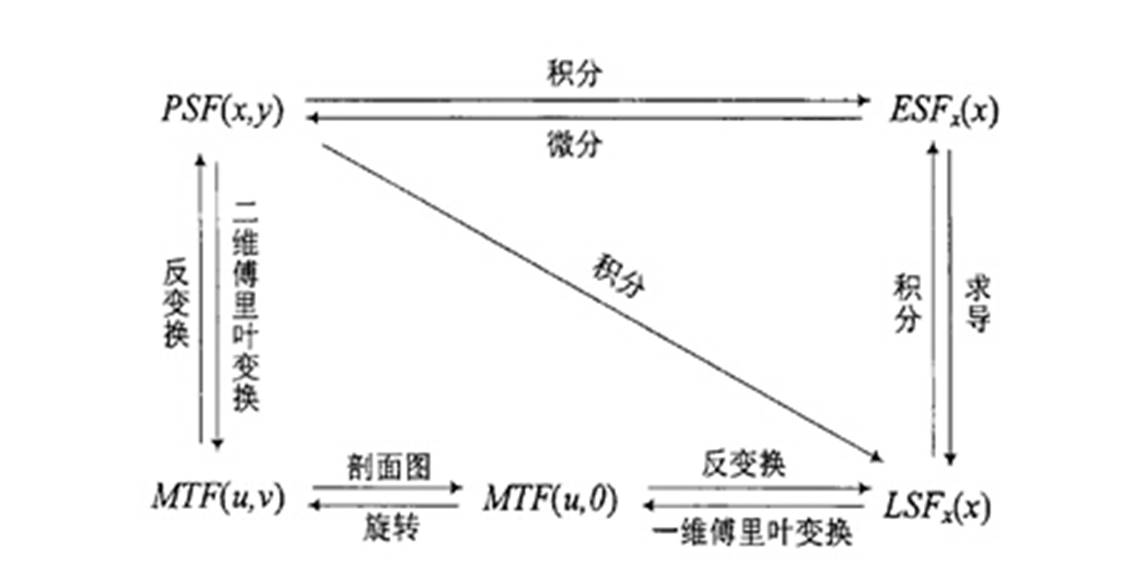
说实话光从这几个数学公式还是不好理解为什么ESF可以求出MTF。换一种角度理解LSF就是一条线上(ESF) 的变化的过称。对于任意一条线由黑变白的过程是由不同频率的黑白线对组成。因此可以反过来通过分析一条线得到这些频率下的 (FFT)。当然这只是一种朴素的理解。后面的文章中会有实际使用的MTF和SFR图卡和测试环境和问题进行进一步讨论
Apr 5, 2016 · 1 minute read · Comments
hardwaresystem
在介绍HDR Sensor原理之前首先讨论为什么需要HDR Sensor.
什么是sensor的动态范围(dynamic range)?
sensor的动态范围就是sensor在一幅图像里能够同时体现高光和阴影部分内容的能力。
用公式表达这种能力就是:
DR = 20log10(i_max / i_min); //dB
i_max 是sensor的最大不饱和电流—-也可以说是sensor刚刚饱和时候的电流
i_min是sensor的底电流(blacklevel) ;
为什么HDR在成像领域是个大问题?
在自然界的真实情况,有些场景的动态范围要大于100dB。
人眼的动态范围可以达到100dB。
Sensor 的动态范围: 高端的 >78 dB; 消费级的 60 dB 上下;
所以当sensor的动态范围小于图像场景动态范围的时候就会出现HDR问题—-不是暗处看不清,就是亮处看不清,有的甚至两头都看不清。
 暗处看不清–前景处的广告牌和树影太暗看不清。
暗处看不清–前景处的广告牌和树影太暗看不清。
 亮处看不清–远处背景的白云变成了一团白色,完全看不清细节。
亮处看不清–远处背景的白云变成了一团白色,完全看不清细节。
解决HDR问题的数学分析
根据前边动态范围公式
DR = 20log10(i_max / i_min); //dB
从数学本质上说要提高DR,就是提高i_max,减小 i_min;
对于10bit输出的sensor, i_max =1023,i_min =1, 动态范围DR = 60;
对于12bit输出的sensor, DR = 72;
所以从数学上来看,提高sensor 输出的bit width就可以提高动态范围,从而解决HDR问题。可是现实上却没有这么简单。提高sensor的bit width导致不仅sensor的成本提高,整个图像处理器的带宽都得相应提高,消耗的内存也都相应提高,这样导致整个系统的成本会大幅提高。所以大家想出许多办法,既能解决HDR问题,又可以不增加太多成本。
解决HDR问题的5种方法
从sensor的角度完整的DR 公式:
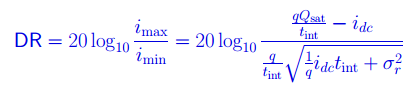
- Qsat :Well Capacity idc: 底电流,tint:曝光时间,σ:噪声。
方法1:提高Qsat –Well capacity 。
就是提高感光井的能力,这就涉及到sensor的构造,简单说,sensor的每个像素就像一口井,光子射到井里产生光电转换效应,井的容量如果比较大,容纳的电荷就比较多,这样i_max的值就更大。普通的sensor well只reset一次,但是为了提高动态范围,就产生了多次reset的方法。
通过多次reset,imax增加到i‘max,上图就是current to charge的转换曲线。
但这种方法的缺点是增加FPN,而且sensor的响应变成非线性,后边的处理会增加难度。
方法2:多曝光合成
本质上这种方法就是用短曝光获取高光处的图像,用长曝光获取阴暗处的图像。有的厂家用前后两帧长短曝光图像,或者前后三针长、中、短曝光图像进行融合
”’
If (Intensity > a) intensity = short_exposure_frame;
If (Intensity < b) intensity = long_exposure_frame;
If (b<Intensity <a) intensity = long_exposure_frame x p + short_exposure_frame x q;
“’
当该像素值大于一个门限时,这个像素的数值就是来自于短曝光,小于一个数值,该像素值就来自于长曝光,在中间的话,就用长短曝光融合。这是个比较简化的方法,实际上还要考虑噪声等的影响。
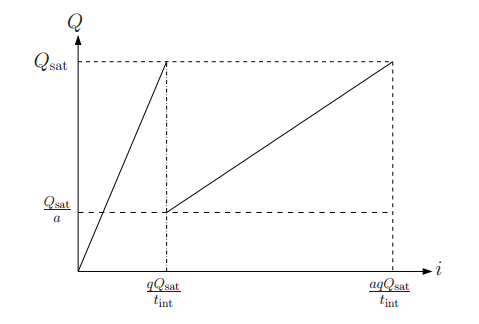
Current to charge曲线显示:imax增加a倍。
这种多帧融合的方法需要非常快的readout time,而且即使readout时间再快,多帧图像也会有时间差,所以很难避免在图像融合时产生的鬼影问题。尤其在video HDR的时候,由于运算时间有限,无法进行复杂的去鬼影的运算,会有比较明显的问题。于是就出现了单帧的多曝光技术。
方法3:单帧空间域多曝光。
最开始的方法是在sensor的一些像素上加ND filter,让这些像素获得的光强度变弱,所以当其他正常像素饱和的时候,这些像素仍然没有饱和,不过这样做生产成本比较高,同时给后边的处理增加很多麻烦。所以下面的这种隔行多曝光方法更好些。
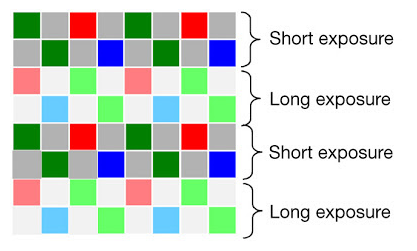
如上图所示,两行短曝光,再两行长曝光,然后做图像融合,这样可以较好的避免多帧融合的问题,从而有效的在video中实现HDR。同时由于video的分辨率比still要低很多,所以这个方法所产生的分辨率降低也不是问题。这个方法是现在video hdr sensor的主流技术。
方法4:logarithmic sensor
实际是一种数学方法,把图像从线性域压缩到log域,从而压缩了动态范围,在数字通信里也用类似的技术使用不同的函数进行压缩,在isp端用反函数再恢复到线性,再做信号处理。
缺点一方面是信号不是线性的,另一方面会增加FPN,同时由于压缩精度要求对硬件设计要求高。
方法5:局部适应 local adaption
这是种仿人眼的设计,人眼会针对局部的图像特点进行自适应,既能够增加局部的对比度,同时保留大动态范围。这种算法比较复杂,有很多论文单独讨论。目前在sensor 端还没有使用这种技术,在ISP和后处理这种方法已经得到了非常好的应用。

上图就是用方法2 + 方法5处理后的HDR图像。亮处与暗处的细节都得到了很好的展现。



![]()
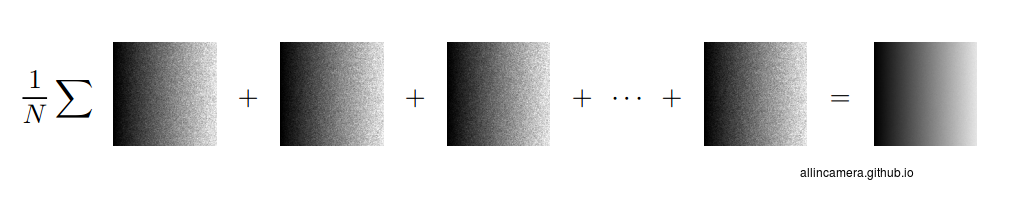

![]()




















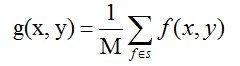























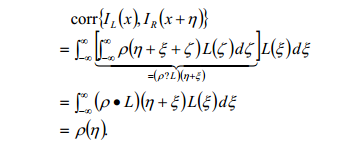
















 暗处看不清–前景处的广告牌和树影太暗看不清。
暗处看不清–前景处的广告牌和树影太暗看不清。
 亮处看不清–远处背景的白云变成了一团白色,完全看不清细节。
亮处看不清–远处背景的白云变成了一团白色,完全看不清细节。