解析力 (2)空间采样 和 奈奎斯特
Apr 6, 2016 · 1 minute read · Commentshardwaresoftwaresystem
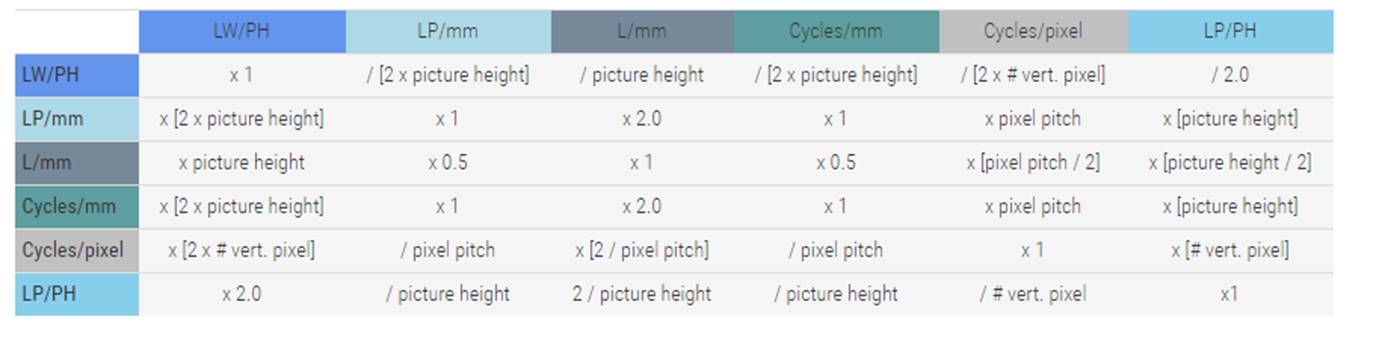
上一篇也说到MTF曲线的时候横坐标是空间频率。一般使用黑白交替的线对来表示空间频率。而空间频率的单位一般是线对每毫米(lp/mm),周期每毫米(cycles/mm),周期每像素(cycles/pixel),线宽每图像高(LW/PH Line Widths per Picture Height),线对每图像高(lp/ph)。其中lp/mm是目前使用最多的单位。cycles/pixel是在数码相机中的成像系统的。数码相机下一个像素就是1 cycles/pixel,两个像素就是0.5 cycles/pixel,4个像素是0.25 cycles/pixel.其它单位的计算如下,纵向是已知横向是未知。
当知道了空间频率的单位之后又有了一个问题。到底用什么样的空间频率去评价MTF合适呢?这个时候经常能看到一个名词奈奎斯特(Nyquist)频率,这是来自采样定律。奈奎斯特和成像有什么关系呢? 数字相机的Sensor在成像过程中就相当与对镜头成的模拟像进行空间数字采样。 奈奎斯特采样定理是指在进行模拟与数字信号的转换过程中,当采样频率大于信号中最高频率的2倍时,采样之后的数字信号完整地保留了原始信号中的信息,但是一般实际应用中保证采样频率为信号最高频率的5~10倍。数码相机的Nyquist取决于pixel 的大小.根据前面给出的空间频率单位转换公式。
对于给定的Pixel size的sensor
Nyquist 频率= 1000[µm]/(pixel_pitch [µm]X2)
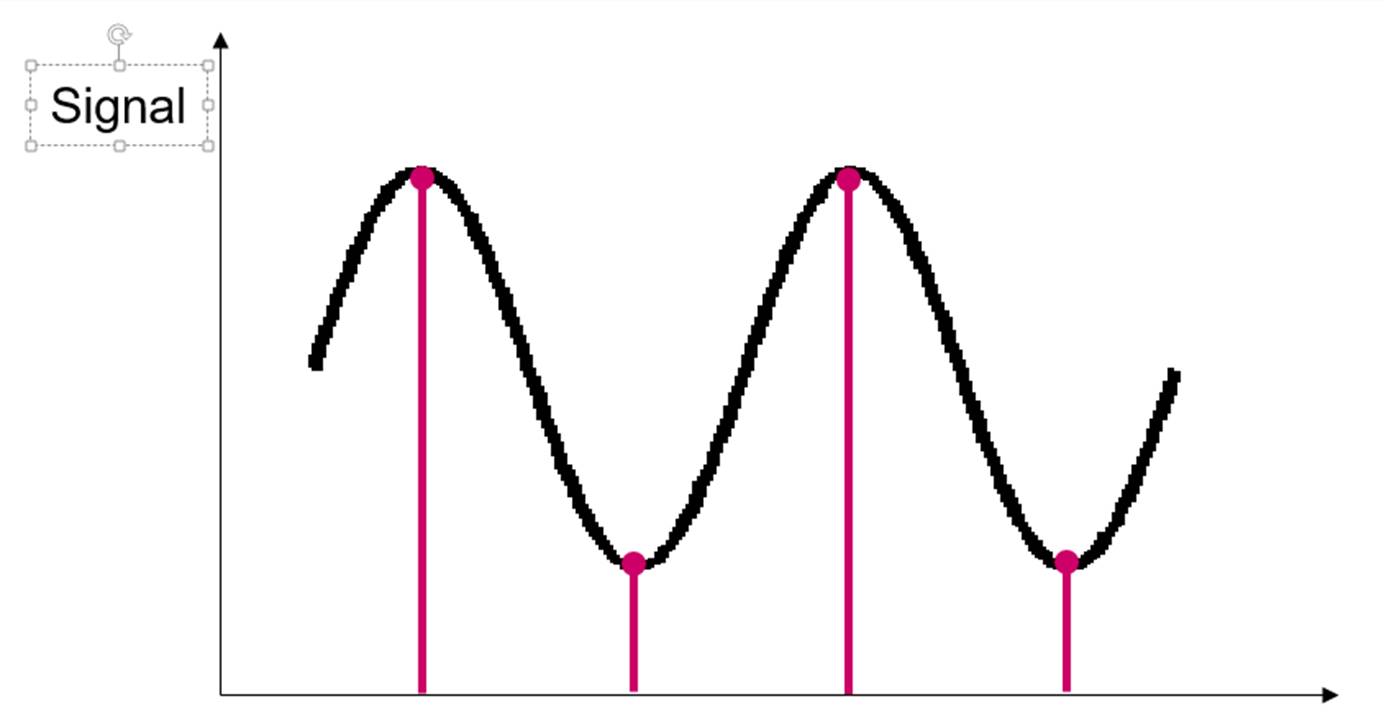
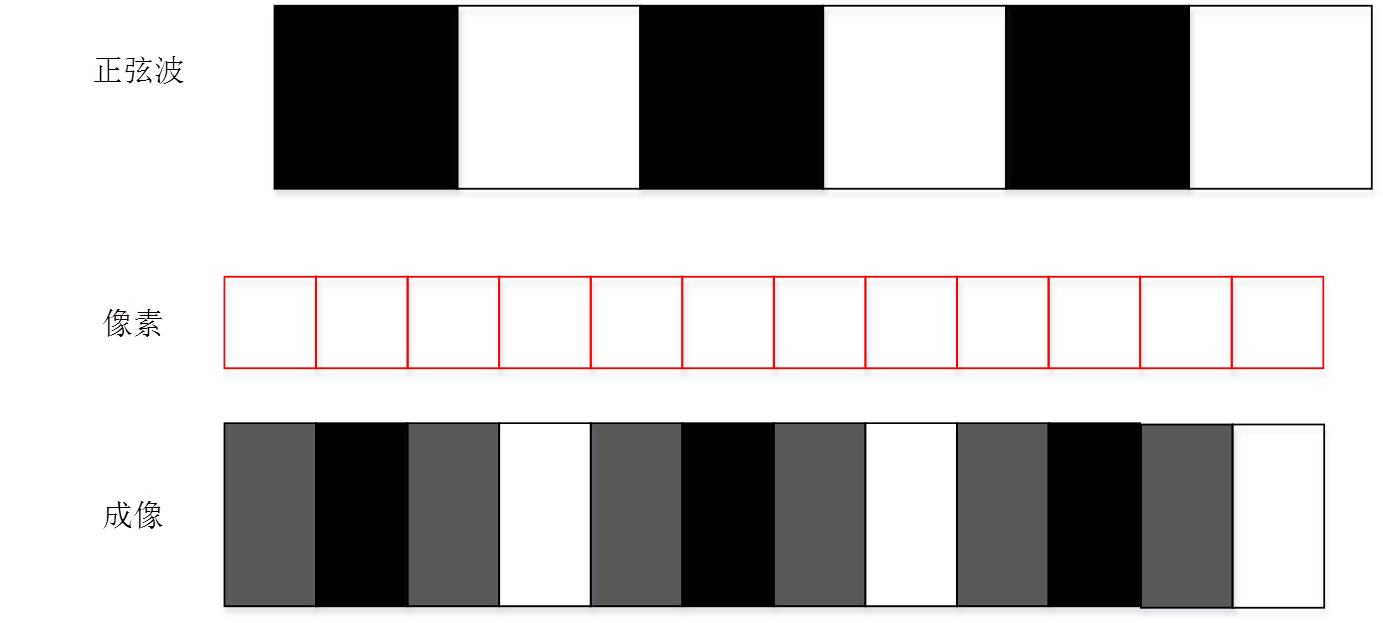
评价MTF使用的奈奎斯特频率(Nyquist频率)是离散信号系统采样频率的一半,也就是一个方向上的像素数一半。采样定理指出,只要离散系统的奈奎斯特频率高于被采样信号的最高频率或带宽,就可以避免混叠现象。但这只是理论上。我们先看下一个接近奈奎斯特频率的频率的采样过程。当然下面的成像过程都是基于一个理想的没有MTF衰减的镜头的情况下。我们实际的像素对正弦图卡的采样过程可以模拟为
![]()
而在采样理论中的采样过程中类似下图。两个采样点之间的周器和数字成像系统的像素一样。但是希望采样点能够尽量小。

采样定理中的只要小于奈奎斯特频率频率都可以被采样还原是有两个条件的。
1采样点的尽量小,而我们的像素大小实际上接近于
2重建信号的过程需要以一个低通滤波器或者带通滤波器将在奈奎斯特频率之上的高频分量全部滤除,同时还要保证原信号中频率在奈奎斯特频率以下的分量不发生畸变。
这两者在图像系统中都很难满足。因此很多时候即使采样过程中信号的最大频率小于奈奎斯特频率频率依然无法很好的得到采样还原。
即使选取一个略小于奈奎斯特频率频率的正弦图卡。当发生相差的时候像素就很有可能无法正确采样出来实际图卡的原来的形状。但是多数情况下使用理想的采样模型是可以将原有信号正确的采样出来的,下面两张图是相差的影响对实际像素的采样影响。
![]()

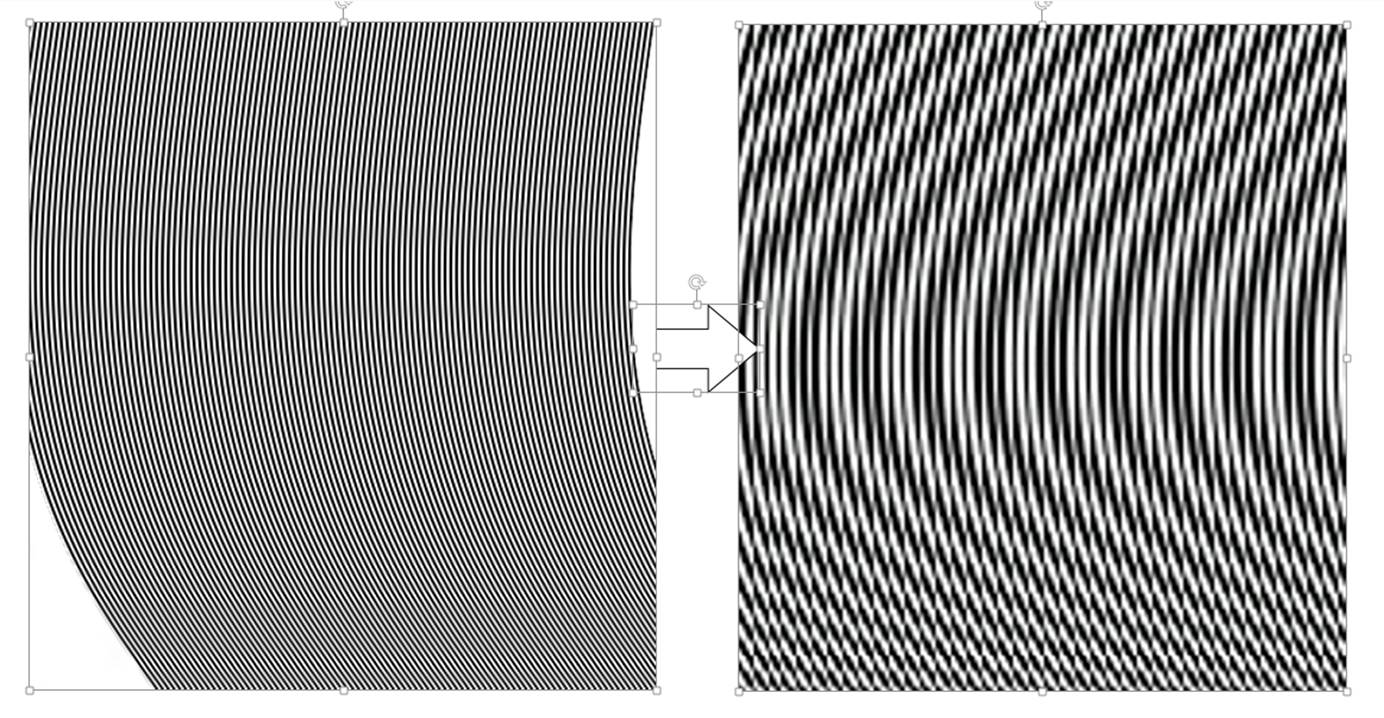
前面提到当频率高于奈奎斯特频率的时候会产生混叠现象。混叠(aliasing) 在信号也称为叠频;在成像上称为叠影,叠影会产生伪纹也就是平常说的摩尔纹。下面的就是一个高于Nyquist频率的频率产生伪纹的采样情况。
![]()
从采样的一般规律来说如果要消除上面这些相差和混叠的影响就需要提高采样的频率。对于常用的采样频率我们可以参考示波器。示波器是一个常用的采样系统,一般示波器的采样频率在被采样频率的5到8倍。但是数字成像系统不同于示波器的是采样的频率在感应器被确定了之后就已经定了。更多的我们是希望知道原有图像在什么频率下分析成像系统的品质更合适。图像采样的过程中肯定是频率越低的图像越清晰。但是一般什么频率的图像是采样的清晰度是应该可以很好的分辨呢。根据如下图一样的仿真和经验,一般能很好分辨的频率在每个线对4个像素左右,也就是1/2奈奎斯特频率.。下面两张图是在1/2 Nyquist频率采样的情况
没有相差的1/2 Nyquist频率采样的情况
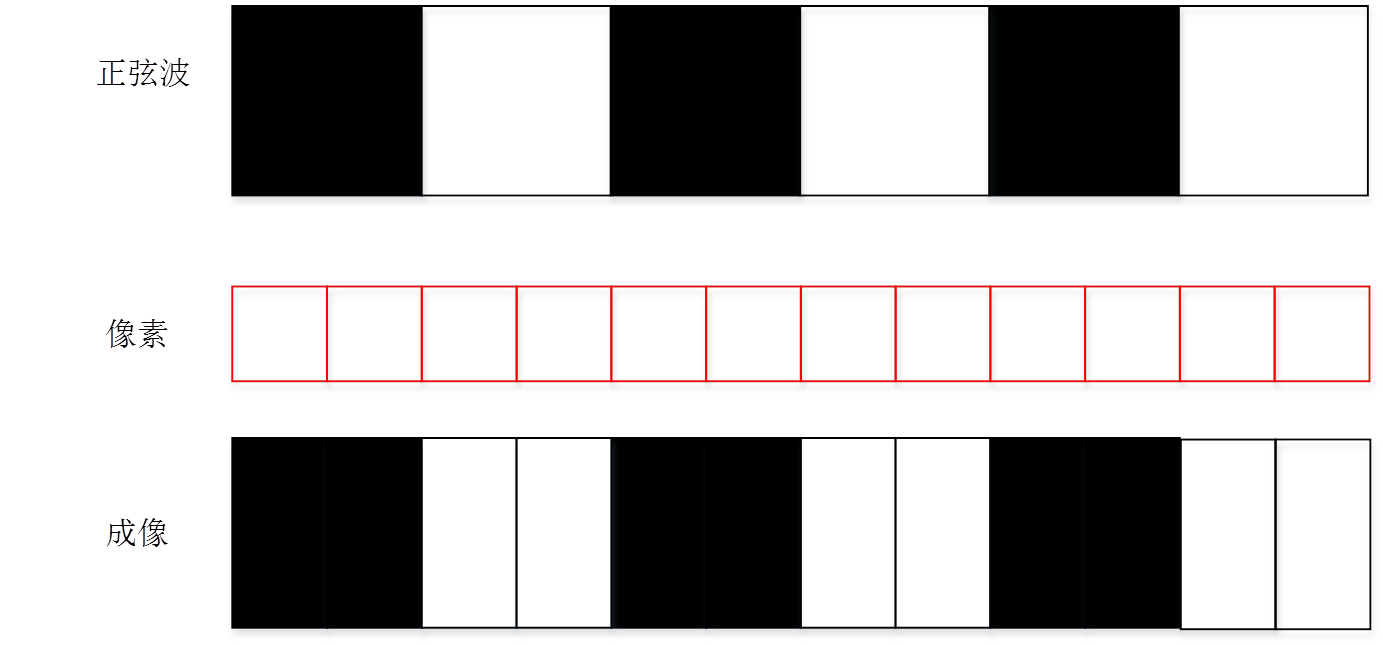
有相差的1/2 Nyquist频率采样的情况
我们可以看到在1/2 Nyquist下即使有相差,也可以基本上还原原有图像的形状了。但是这只是仿真像素的采样过程中,在实际测试过程中由于镜头,噪声和测试环境影响在1/2奈奎斯特频率附近测试MTF值很不稳定。因此也经常选取更低1/4奈奎斯特频率作为MTF测试值所选取的频率。不过MTF的评价并不是简单的看一个频率就可以评价一个成像系统的效果,MTF曲线是一个整体。下一篇中将介绍怎么来通过SFR算法得到MTF曲线评价一个手机模组。