图解噪声与去噪之三:噪声建模与去噪
May 21, 2016 · 1 minute read · Commentshardwaresoftwaresystem
本文系微信公众号『大话成像』,知乎专栏『All in Camera』原创文章,转载请注明出处。
上一篇说到bm3d等高级算法可以利用数学方式把信号分解成不同性质的部分,然后根据不同的噪声特点进行去噪。噪声模型则是去噪算法的重要依据。
先看一个实验,拍摄一张Grey Scale Chart:

曝光时间 33ms, ISO 3200,得到如下图像:

图像上有很多噪声,对这个图像做横切,可以得到pixelvalue相对intensity的关系图

![]()
继续拍摄至N张照片,将N张照片求平均得到一张照片
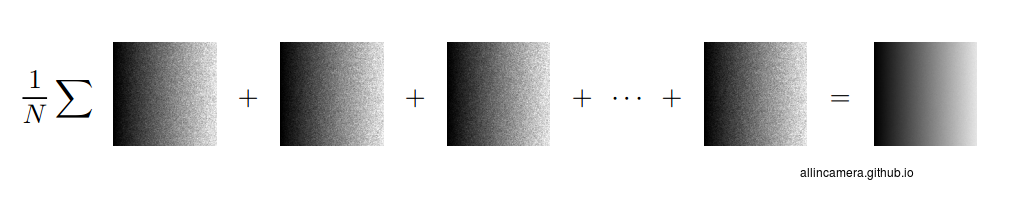
求和平均得到的照片

把所有图片的像素值与亮度标在一个图中
![]()
中间的实线是图像均值,所有被虚线包围的红色的点,是所有图像的像素值。
按照图解噪声与去噪第一篇里的方法,画出像素标准差对均值的曲线可以得到
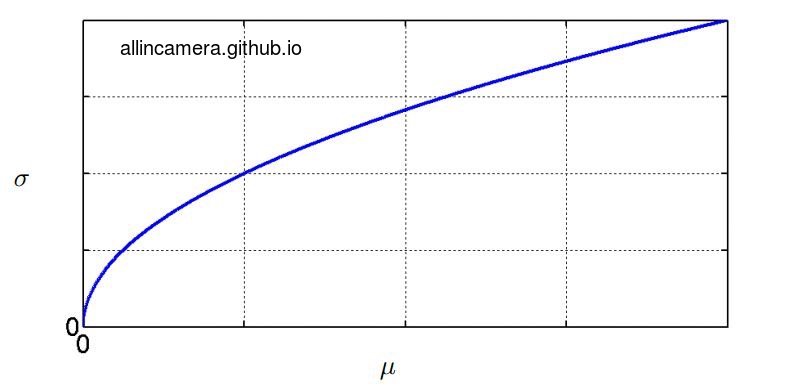
从上图可以看出: 1. 噪声随着亮度的增加而增加。 2. 标准差与均值遵循一定的函数关系。
把多组实验的结果叠加可以得到下图:
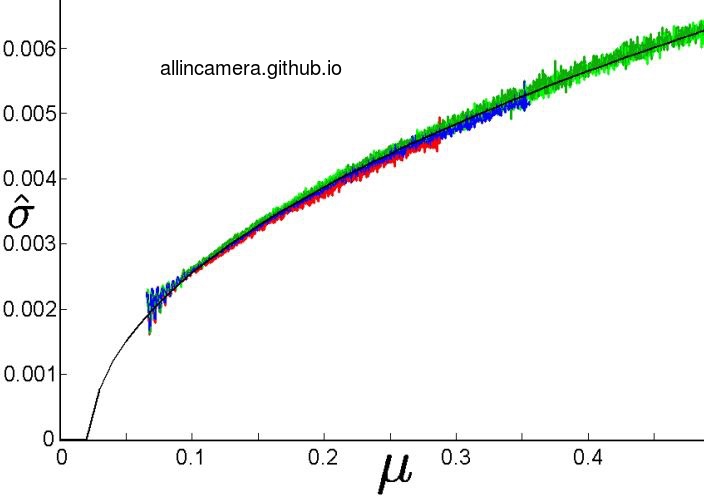
可以看出在平滑的曲线上多了许多毛刺.
从上面两张图可以看出在图像中存在着两种噪声:信号相关噪声,信号不相关噪声。平滑上升的曲线是随信号均值上升的,而毛刺是不随信号均值增大的。
数学上把这两种噪声用泊松分布模型和高斯分布模型来描述:
y = α Pi + ni, pi ~ P(x), Ni ~ N(0,σ2),
y是总噪声,α是量化参数,Pi是泊松噪声,Ni是高斯噪声,x是信号。Pi是信号相关的,Ni是信号不相关的。
以上证明了噪声模型的数学实现性,真正应用的噪声模型比上述基本模型要复杂一些。有了噪声的数学模型,就可以用统计学的方法,针对这两种不同的噪声模型进行处理。 具体的过程如下:
1> 先得到一个sensor的噪声profile(标准差 对 亮度)
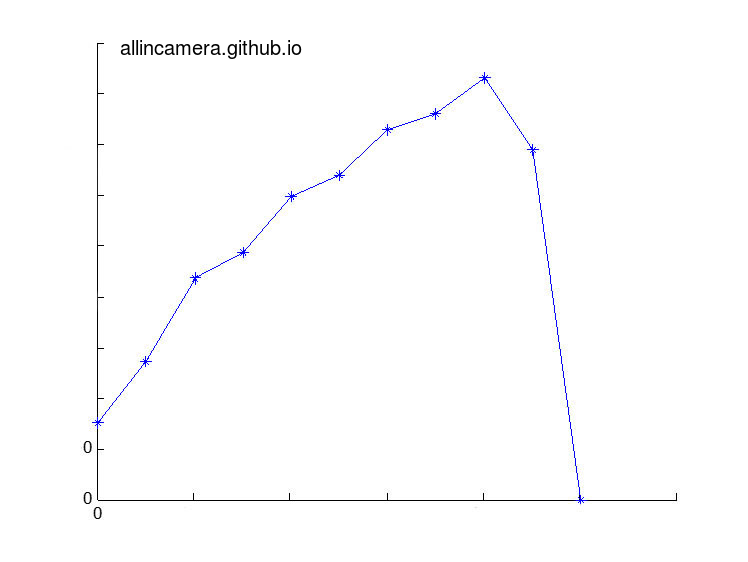
2> 利用之前说的泊松-高斯模型做curve fitting
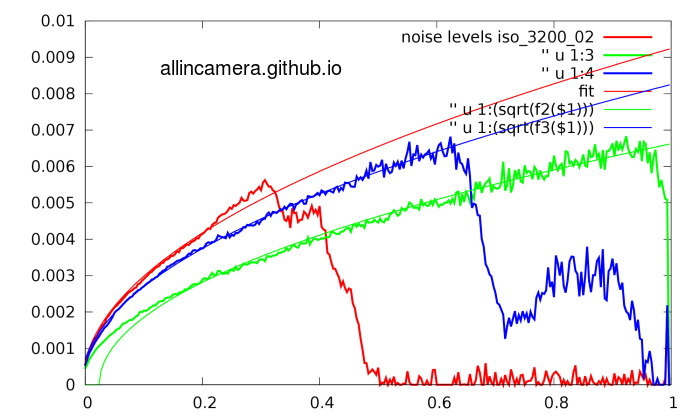
RGB三个通道有三个不同的响应,三个不同的fitting曲线。
3> Variance Stabilization
在噪声建模的论文中都用这个词Stabilization–稳定化。实际上我的理解就是把噪声对亮度做‘归一化’。因为在现在的信号处理方法中,信号依赖性的噪声处理起来非常不便。所以需要把噪声对亮度做归一化。这样就需要根据前边的fitting curve产生conversion function curve。
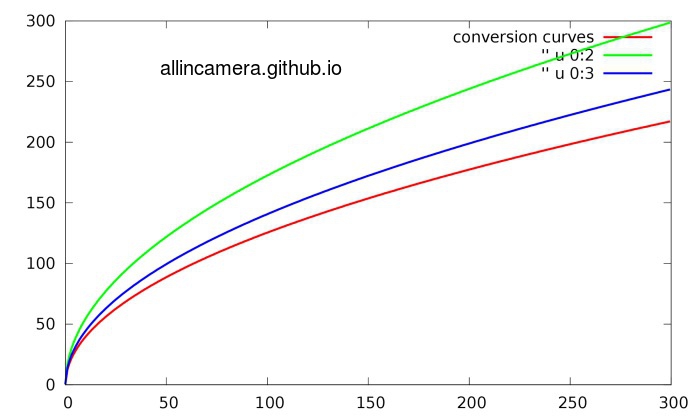
4> 把conversion function curve 作用到原始信号就会得到噪声归一化的信号:
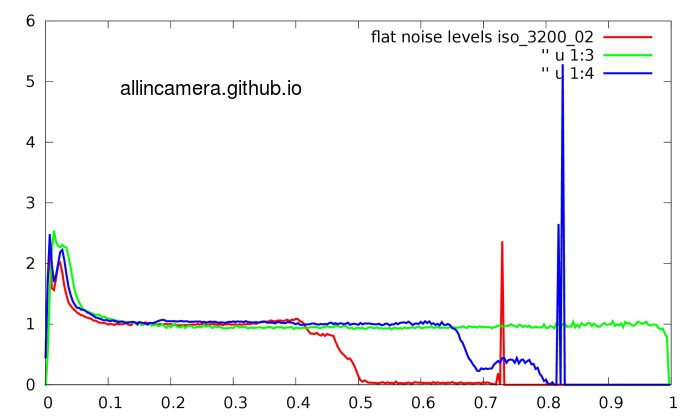
5> 用常用的去噪方法,比如wiener filter and dct, bm3d, wavelet-based 方法, nlmeans 进行去噪
6> 做完去噪,再做反变换,就可以恢复成原始的信号
参考文献:
markku makitalo, alessandro foi: optimal inversion of the generalized anscombe transformation for poisson-gaussian noise, ieee trans. image process
alessandro foi et al.: practical poissonian-gaussian noise modeling and fitting for single-image raw-data, ieee trans. image process. vol. 17, no. 10, 2008.
k. dabov, a. foi, v. katkovnik, and k. egiazarian: image denoising with block-matching and 3d filtering. proc. spie electronic imaging, 2006.
Alessandro Foi是芬兰Tampere大学研究图像去噪和噪声建模的教授,他的文章谈到的方法很多都已经在手机camera中得到了应用,具有很高的参考价值。
本文系微信公众号『大话成像』,知乎专栏『All in Camera』原创文章,转载请注明出处。