图解噪声与去噪 之一： fix pattern noise（FPN）与 temporal noise

Apr 19, 2016 · 2 minute read · Comments
software

本文系微信公众号《大话成像》，知乎专栏《大话成像 all in camera》原创文章，转载请注明出处。

噪声分类

噪声有很多种分类方法，比如从频率上分，可以分为高频，中频，低频噪声。

从色彩空间上分，可以分为luma noise亮度噪声与chroma noise彩色噪声。

从时态上分，可以分为fix pattern noise与temporal noise。Fix pattern noise 与时间无关，表现上看就是噪声幅度不随时间变化。Temporal noise是随时间变化，在低光下录制的视频中不断变化的细小信号就是temporal noise。

也有的分法把fix pattern noise定义为在图像行或者列存在的一条条的噪声，如下图所示。

Temporal noise视觉上是一种高频噪声。

噪声计算

均值 $\mu = \dfrac {\sum^{n}_{i=1}X_{i}}{n}$

标准差 $\sigma=\dfrac {1}{n-1}\sum ^{n}_{i=1}\left(u-x{i}\right)^{2}$

图像的标准差可以作为图像噪声水平的评价值。

按照如下曝光时间，每个曝光时间拍30张black 照片。

	exp_time = [0.063, 1.003,16, 64,257,513,770,1027,1283,1540,1797,2054];
	raw_avg = 0;
	for kk = 0:30:(30*12-1)
	    for i = 1:30
	        fname = fileNames{kk+i};      
	        fprintf('processing %s %d\n', fname, kk+i);
	        raw = double(imread([fold fname]));
	        raw = raw(:,:,1);
	        raw_avg = raw + raw_avg;  
	    end
	    raw_avg = raw_avg./30; 
	    
	    avg_signal((kk/30)+1) = round(mean2(raw_avg));
	    fpn_total((kk/30)+1) = std2(raw_avg);
	     
	    fpn_col_exp((kk/30)+1) = std(mean(raw_avg,1));
	%     avg_sig_col_exp((kk/30)+1,:) = mean(raw_avg,1);
	    
	    fpn_row_exp((kk/30)+1)     = std(mean(raw_avg,2)');
	%     avg_sig_row_exp((kk/30)+1) = mean(raw_avg,2)';

如上计算，可以得到图像的平均信号，每个曝光的FPN noise，以及行，列FPN noise,行列均值。

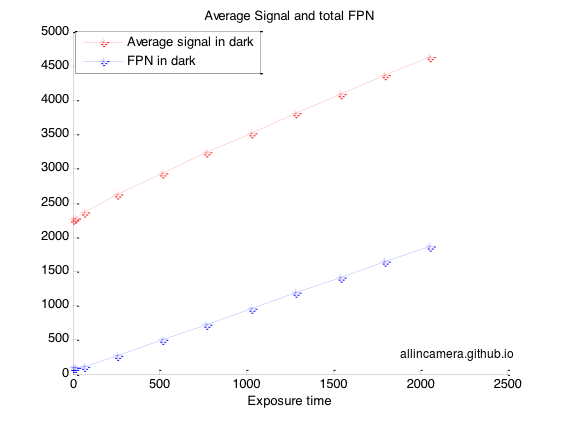
把曝光逐渐增加，确保图像能够达到饱和，在10个曝光值，每个曝光值下拍30张flat field照片

	raw_avg = 0;
	temp_noise = zeros(30,480*752);
	for kk = 0:30:(30*11-1)
	    for i = 1:30
	        fname = fileNames{kk+i};
	        fprintf('processing %s %d\n', fname, kk+i);
	        raw = double(imread([fold fname]));
	        raw = raw(:,:,1);
	        raw_avg = raw + raw_avg;
	        temp_noise(i,:) = raw(:)';
	    end
	    raw_avg = raw_avg./30;
	    
	    std_temp_noise = std(temp_noise,1);
	    
	    avg_signal((kk/30)+1) = round(mean2(raw_avg));
	    temporal_total((kk/30)+1) = median(std_temp_noise);

如上计算，可以得到图像的temporal noise

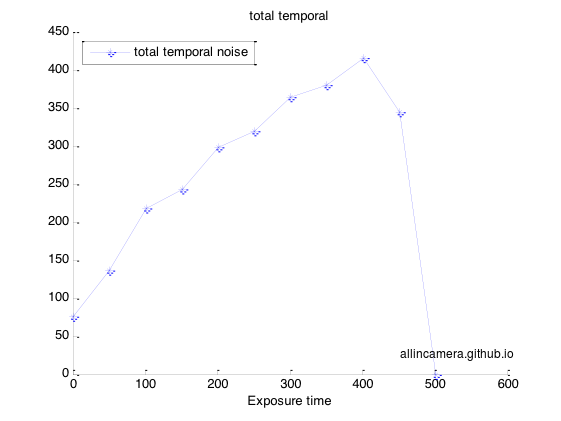
最后图像饱和，所以噪声降低至0。

FPN noise是相关噪声，temporal noise是不相关噪声。

两个图像相加：

$S = S_1 + S_2$ S代表信号

$\sigma^{2}_{t}=\sigma^{2}_{t1}+\sigma^{2}_{t2}$ $\sigma_{t}$ 代表temporal noise

信噪比SNR $\dfrac {S}{\sigma_{t}}=\dfrac {S_{1}+S_{2}}{\left(\sigma^{2}_{t1}+\sigma^{2}_{t2}\right)^{0.5}}$

当 $S_{1} = S_{2}$ , $\sigma_{t1} = \sigma_{t2}$, 信噪比SNR $\dfrac {S}{\sigma_{t}}=2^{0.5}\dfrac{S_{1}}{\sigma_{t1}}$

当 $S_{1} = S_{2}=...=S_{n}$ , 信噪比SNR $\dfrac {S}{\sigma_{t}}=n^{0.5}\dfrac{S_{1}}{\sigma_{t1}}$

该公式从理论上证明了n帧平均会降低temporal noise $n^{0.5}$ 倍。所以信号处理中去除temporal noise的方法就是多帧平均加运动检测，如果存在图像存在变化就不累加，如果图像无变化就累加平均。

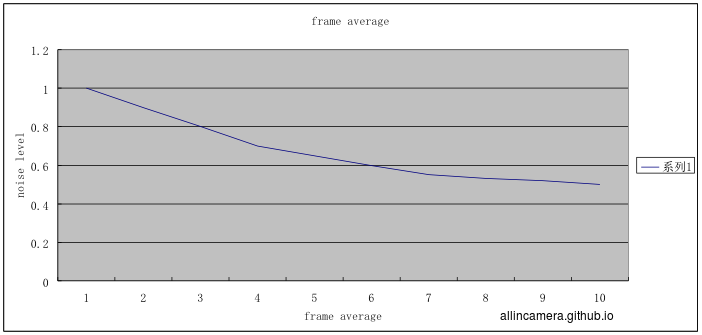
而FPN noise 是相关噪声

$\sigma_{fpn} = \sigma_{fpn1} + \sigma_{fpn2}$

$S = S_{1} + S_{2}$

$ \dfrac {S}{\sigma_{fpn}} = \dfrac {S_{1}+S_{2}}{\sigma_{fpn1}+\sigma_{fpn2}} $

当 $ S_{1} = S_{2} $, $ \sigma_{fpn1} = \sigma_{fpn2} $ 时， $ \dfrac {S}{\sigma_{fpn}} = \dfrac {S_{1}}{\sigma_{fpn1}} $

多帧平均不会降低FPN。

通过上图可以看出，经过多帧平均后，噪声的floor变成了FPN。

通过多帧平均可以分离temporal noise和FPN，然后用其他信号处理的方法去除FPN，下一篇将介绍去噪的Spacial domain 和 transform domain的方法。