反差式对焦评价函数的频率特性考虑
Apr 7, 2016 · 1 minute read · Commentshardwaresoftwaresystem
当前手机成像系统中普遍使用反差式对焦系统,也就是计算当前图像的锐度,依照图像锐度与镜头位置的关系,寻找最锐度最高的镜头位置作为合焦位置的方法。在搜索策略上各厂商基本相似,在锐度提取也就是清晰度的计算上,应该根据光学特性的不同做差异化设计。
基于芯片硬件设计的方便性考虑,大部分的锐度评价函数都设计为一个m x n算子,记作P,算子的填充决定其特性:一般是高通,或者是带通滤波器。如果图像记作G,那么图像的锐度S可以表示为: S = P * G P 对 G 做卷积。
高通与带通滤波器的优缺点
高通滤波器对高频成分很敏感,当成像系统离焦不远时,图像高频成分很容易被提取出来,随着镜头的移动,计算出锐度的差异很明显。但是当图像离焦很远时,比如对焦的物体消失,背景物体又在远处,高通滤波器对图像的响应就不明显,这样镜头移动计算出的锐度变化就不明显,造成搜索失败。
如下图
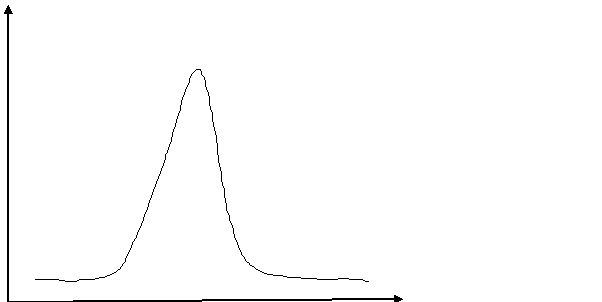
当锐度值在曲线两侧,无论镜头如何移动,变化都非常不明显,这样搜索算法就很难工作,这个评价函数就是不合适的。为了解决这个问题,就需要在设计滤波器P的时候,让低频成分多通过一些。
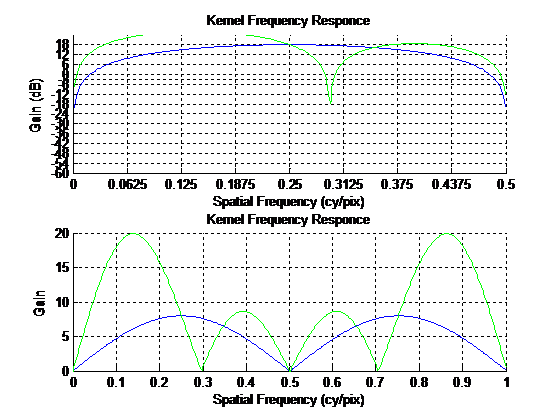
蓝色的曲线是滤波器P1的频率响应,绿色的曲线是滤波器P2的频率响应,相比可见,绿色曲线可以让更多低频成分通过。
选择一个滤波器后,需要根据实际图像进行计算仿真,画出这个滤波器对不同离焦程度图像卷积所产生的锐度值
kern = [-1 -2 -3 -5 -8;8 5 3 2 1];%c
% kern = [-1 0 1; -2 0 2; -1 0 1];%r
% kern = [ -1 -1 -1;-1 0 1;1 1 1];%g
% kern = [ -1 -1 -1;-1 8 -1;-1 -1 -1];%b
% kern = [ 7 5 -1 0 -1 ;1 0 -5 1 -7]; %m
kern = [ 6 0 6 0 0 ;0 -12 0 0 0];%k
% kern = [-5 -4 0 4 5;-8 -10 0 10 8;10 -20 0 20 0;-8 -10 0 10 8;-5 -4 0 4 5]%y
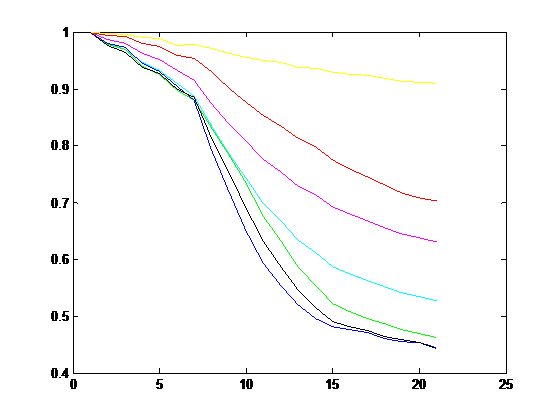
上图就是上面的各个滤波器的仿真结果,横坐标是离焦程度,从0到25,离焦程度逐步变大。纵坐标是计算出的锐度值,1表示最大。通过这个曲线,可以看出对不同离焦程度图像滤波器的响应,依据响应曲线的特点进行选择。